hdu 4267 A Simple Problem with Integers(樹形結構-線段樹)
A Simple Problem with Integers
Time Limit: 5000/1500 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 3708 Accepted Submission(s): 1139
Problem Description
Let A1, A2, ... , AN be N elements. You need to deal with two kinds of operations. One type of operation is to add a given number to a few numbers in a given interval. The other is to query the value of some element.
Input
There are a lot of test cases.
The first line contains an integer N. (1 <= N <= 50000)
The second line contains N numbers which are the initial values of A1, A2, ... , AN. (-10,000,000 <= the initial value of Ai <= 10,000,000)
The third line contains an integer Q. (1 <= Q <= 50000)
Each of the following Q lines represents an operation.
"1 a b k c" means adding c to each of Ai which satisfies a <= i <= b and (i - a) % k == 0. (1 <= a <= b <= N, 1 <= k <= 10, -1,000 <= c <= 1,000)
"2 a" means querying the value of Aa. (1 <= a <= N)
Output
For each test case, output several lines to answer all query operations.
Sample Input
4
1 1 1 1
14
2 1
2 2
2 3
2 4
1 2 3 1 2
2 1
2 2
2 3
2 4
1 1 4 2 1
2 1
2 2
2 3
2 4
Sample Output
1
1
1
1
1
3
3
1
2
3
4
1
首先，我們來設計一下頂層模型。看下圖：
假設我們先插入了3段：
L1 R1 k1 c1
L2 R2 k2 c2
L3 R3 k3 c3
然後查詢圖中的i點，那麼，我只要遍歷所有插入的線段裡包含i點的線段，然後判斷(i-L)%k是否==0，若等於0，就將i點的初始值加上c。
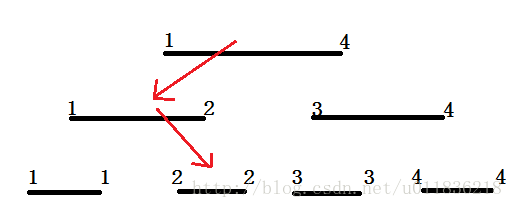
實現：暴力實現肯定會超時，超時就在於找包含i點的線段上。我們可以用線段樹來解決尋找包含i點的線段的問題。見下圖：
vc/ytcTH6b/2o6y1q8rHtbHSqs3509K2+dfTt73P8rXEx+m/9rXEyrG68rvh09DSu7j2zsrM4qOsv7TPwsPmtcTA/dfToaMKvNnJ6M7Sw8ey5cjro7oKYSBiIGsgYwoyIDQgMiAxCjxpbWcgc3JjPQ=="http://img.blog.csdn.net/20140829233120412?watermark/2/text/aHR0cDovL2Jsb2cuY3Nkbi5uZXQvdTAxMTgzNjIxOA==/font/5a6L5L2T/fontsize/400/fill/I0JBQkFCMA==/dissolve/70/gravity/SouthEast" alt="\">
我們發現一個問題，就是當[2,4]往右子樹走時，區間變成了[3,4]，但是[3,4]這個區間的左邊界L=3，(L-a)%k = (3-2)%2 != 0，這樣一來，我們查詢點3的時候就會錯，因為查詢點3時，經過[3,4]，(3-3)%2 == 0那麼答案會+1，但是(3-2)%2 !=0。因此，我們插入的時候必須保證左端點(L-a)%k 一定等於0。所以，當往右邊走的時候，要對區間稍作處理，一般我們會這樣寫：
update(mid+1 , r , 2*k+1)；
現在是：
int tl = mid+1+(k-(mid+1)%k)%k;
update(tl , r , 2*k+1);
當然tl<=r，否則就不必往下插入了。
#include
#include
using namespace std;
const int maxn = 50010;
struct tree{
int l , r, k[12];
}a[4*maxn];
int num[maxn] , N , Q;
void build(int l , int r , int k){
a[k].l = l;
a[k].r = r;
for(int i = 0; i < 12; i++) a[k].k[i] = 0;
if(l != r){
int mid = (l+r)/2;
build(l , mid , 2*k);
build(mid+1 , r , 2*k+1);
}
}
void update(int l , int r , int k , int lk , int lc){
if(l <= a[k].l && a[k].r <= r) a[k].k[lk] += lc;
else{
int mid = (a[k].l+a[k].r)/2;
if(mid >= r) update(l , r, 2*k , lk , lc);
else if(mid < l) update(l , r , 2*k+1 , lk , lc);
else{
update(l , mid , 2*k , lk , lc);
int tl = mid+1+(lk-(mid+1-l)%lk)%lk;
if(tl <= r) update(tl , r , 2*k+1 , lk , lc);
}
}
}
int getAns(int k , int i){
int ans = 0;
for(int j = 1; j <= 10; j++){
if((i-a[k].l)%j == 0) ans += a[k].k[j];
}
return ans;
}
int query(int l , int r , int k){
if(l <= a[k].l && a[k].r <= r) return getAns(k , l);
else{
int mid = (a[k].l+a[k].r)/2;
int ans = getAns(k , l);
if(mid >= r) return ans+query(l , r , 2*k);
else return ans+query(l , r , 2*k+1);
}
}
void computing(){
for(int i = 1; i <= N; i++) scanf("%d" , &num[i]);
build(1 , N , 1);
scanf("%d" , &Q);
int op , la, lb , lk , lc;
while(Q--){
scanf("%d" , &op);
if(op == 1){
scanf("%d%d%d%d" , &la , &lb , &lk , &lc);
update(la , lb , 1 , lk , lc);
}else{
scanf("%d" , &la);
printf("%d\n" , num[la]+query(la , la , 1));
}
}
}
int main(){
while(~scanf("%d" , &N)){
computing();
}
return 0;
}
