程式師世界 >> 編程語言 >> C語言 >> C++ >> C++入門知識 >> UVA - 12075 Counting Triangles

UVA - 12075 Counting Triangles

編輯：C++入門知識

UVA - 12075 Counting Triangles

Description

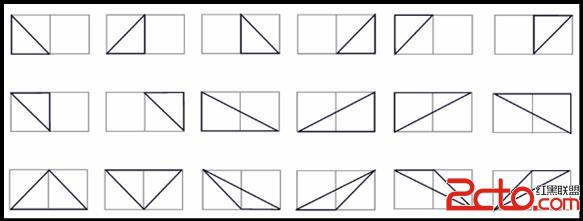
Triangles are polygons with three sides and strictly positive area. Lattice triangles are the triangles all whose vertexes have integer coordinates. In this problem you have to find the number of lattice triangles in anMxN grid. For example in a (1x 2) grid there are 18 different lattice triangles as shown in the picture below:

$\epsfbox{p3295.eps}$

Input

The input file contains at most 21 sets of inputs.

Each set of input consists of two integers M andN ( 0 < M, N $\le$ 1000 ). These two integers denote that you have to count triangles in an (MxN) grid.

Input is terminated by a case where the value of M andN are zero. This case should not be processed.

Output

For each set of input produce one line of output. This output contains the serial of output followed by the number lattice triangles in the(MxN) grid. You can assume that number of triangles will fit in a 64-bit signed integer.

Sample Input

1 1
1 2
0 0

Sample Output

Case 1: 4
Case 2: 18
題意： 給你n*m的網格，問你能有幾個三角形。
思路： 我們先計算任意三個點組成的可能，然後排除同一水平，同一垂直的，同一斜線的，前兩個比較好計算，同一斜線的稍復雜。
同一斜線的和上一題UVA - 1393 Highways 一樣也是要用容斥原理，首先我們動手計算一下，可能發現每次多的是gcd(i, j)-1,然後再去重，dp[i][j]代表從左上角[0,0]
到這個點[i,j]並以這兩個點為端點枚舉三點共線的個數，最後還要遞推一次，得到n*m的網格三點共線的個數，當然這也要*2，感覺怪怪的，瞎搞過的

#include  #include  #include  #include  #includetypedef long long ll; using namespace std; const int maxn = 1010; ll dp[maxn][maxn], ans[maxn][maxn]; int n, m; int gcd(int a, int b) { return b==0?a:gcd(b, a%b); } void init() { memset(dp, 0, sizeof(dp)); memset(ans, 0, sizeof(ans)); for (int i = 1; i < maxn; i++) for (int j = 1; j < maxn; j++) dp[i][j] = dp[i-1][j] + dp[i][j-1] - dp[i-1][j-1] + gcd(i, j) - 1; for (int i = 1; i < maxn; i++) for (int j = 1; j < maxn; j++) ans[i][j] = ans[i-1][j] + ans[i][j-1] - ans[i-1][j-1] + dp[i][j]; } ll cal(int x) { if (x < 3) return 0; return (ll) x * (x - 1) * (x - 2) / 6; } int main() { init(); int cas = 1; while (scanf("%d%d", &n, &m) != EOF && n + m) { printf("Case %d: ", cas++); ll sum = cal((n+1)*(m+1)) - (m+1)*cal(n+1) - (n+1)*cal(m+1) - ans[n][m] * 2; printf("%lld\n", sum); } return 0; }