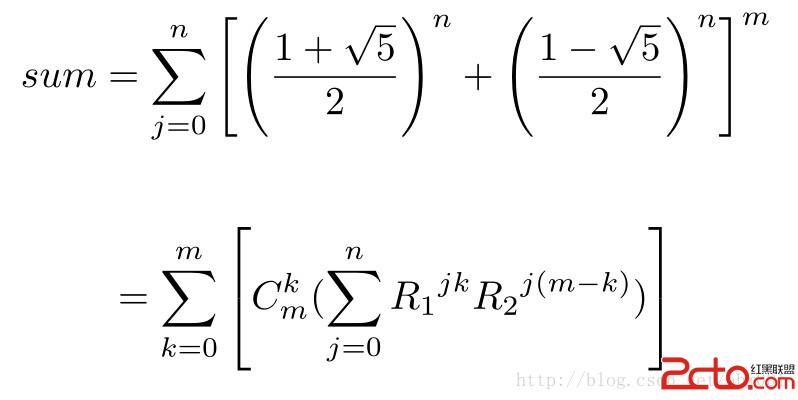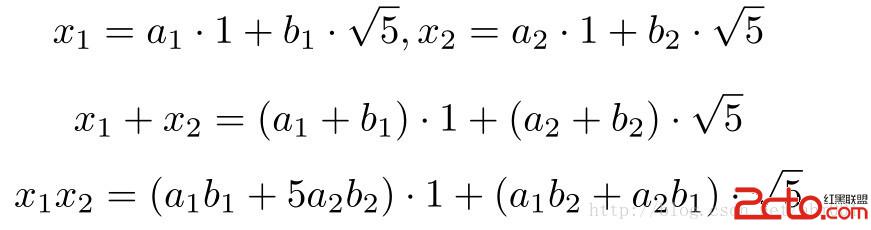[hdu 4959]Poor Akagi 數論(盧卡斯數,二次域運算,等比數列求和)
Poor Akagi
Time Limit: 30000/15000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 131 Accepted Submission(s): 29
Problem Description
Akagi is not only good at basketball but also good at math. Recently, he got a sequence Ln from his teacher. Ln is defined as follow:
$$\Large L(n)=\begin{cases}
2 & \text{ if } n=0 \\
1 & \text{ if } n=1 \\
L(n-1)+L(n-2) & \text{ if } n>1
\end{cases}$$
And Akagi’s teacher cherishes Agaki’s talent in mathematic. So he wants Agaki to spend more time studying math rather than playing basketball. So he decided to ask Agaki to solve a problem about Ln and promised that as soon as he solves this problem, he can
go to play basketball. And this problem is:
Given N and K, you need to find \(\Large\sum\limits_{0}^{N}L_i^K\)
And Agaki needs your help.
Input
This problem contains multiple tests.
In the first line there’s one number T (1 ≤ T ≤ 20) which tells the total number of test cases. For each test case, there an integer N (0 ≤ N ≤ 10^18) and an integer K (1 ≤ K ≤ 100000) in a line.
Output
For each test case, you need to output the answer mod 1000000007 in a line.
Sample Input
3
3 1
2 2
4 3
Sample Output
10
14
443
Source
BestCoder Round #5
題目大意
求盧卡斯數的k次方的前n項和
盧卡斯數為L[0]=2,L[1]=1,L[n]=L[n-2]+L[n-1](n>=2)
題目思路
當時看到題還以為直接根據 zoj 3774 找出二次剩余…… 結果發現1e9+7不存在二次剩余
最後發現了一種很巧妙的做法
直接根據盧卡斯數的通項公式
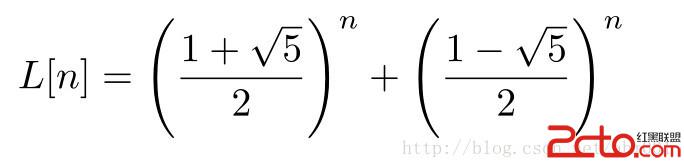
設
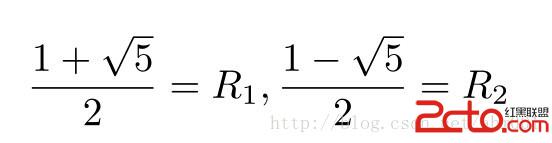
則求和公式為
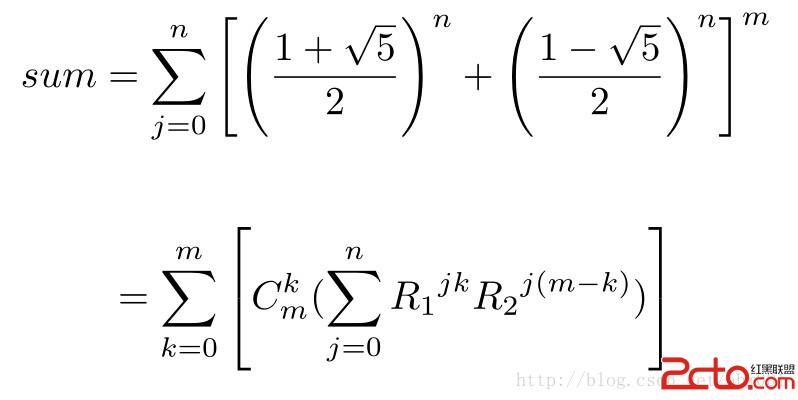
定義二次域
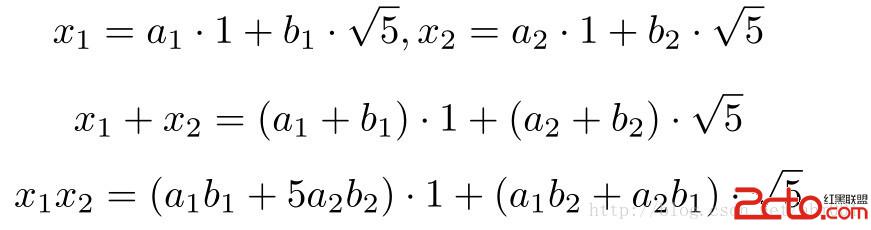
此時直接對二次域進行加、乘操作即可(最後的結果為整數,故根號五不會存在在結果之中)
重載二次域的加號和乘號,定義二次域的快速冪運算,全部帶入公式即可。
=.=好像這一題的杭電的數據還沒有修正
公比為一時直接返回n+1(可能帶來溢出)竟然AC了
然後正解依然WA……
這裡只放正解代碼
/**
**author : ahm001 **
**source : hdu 4959**
**time : 08/21/14 **
**type : math **
**/
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
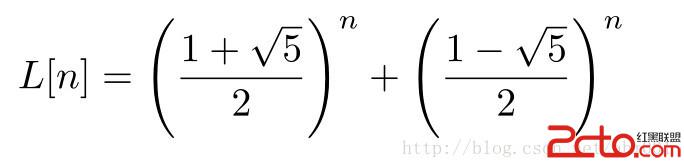
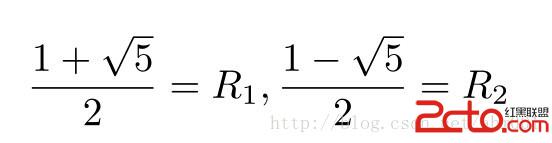 則求和公式為
則求和公式為