UVA - 1393 Highways

UVA - 1393 Highways

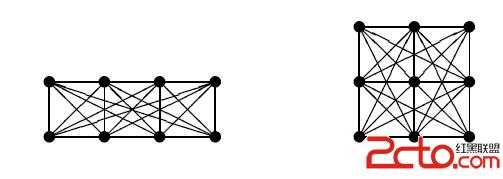
Description

Hackerland is a happy democratic country with m×n cities, arranged in a rectangular m by n grid and connected by m roads in the east-west direction and n roads in the north-south direction. By public demand, this orthogonal road system is to be supplemented by a system of highways in sucha way that there will be a direct connection between any pair of cities. Each highway is a straight line going through two or more cities. If two cities lie on the same highway, then they are directly connected.If two cities are in the same row or column, then they are already connected by the existing orthogonal road system (each east-west road connects all the m cities in that row and each north-south road connects all the n cities in that column), thus no new highway is needed to connect them. Your task is to count the number of highway that has to be built (a highway that goes through several cities on a straight line is counted as a single highway).

Input

The input contains several blocks of test cases. Each test case consists of a single line containing two integers 1n , m300 , specifying the number of cities. The input is terminated by a test case with n = m = 0 .

Output

For each test case, output one line containing a single integer, the number of highways that must be built.

Sample Input

2 4
3 3
0 0

Sample Output

12
14
題意：有一個n行m列的點陣，問一共有多少條非水平非豎直的直線至少穿過其中的兩個點。
思路：這題分兩步，首先計算出從點[1, 1]到[n, m]格子組成的邊界的連線，然後這是需要容斥去重的，這個有新的數能加的可能是當維度i和j是互質的時候就會多一個，
然後就是遞推n*m的格子的總個數，也要容斥去重，這個就是減去減半的數，這個是因為會重線，最後是對稱，從左上到右下，和從坐下到右上
#include 
#include 
#include 
#include 
typedef long long ll;
using namespace std;
const int maxn = 310;

int n, m;
ll dp[maxn][maxn], ans[maxn][maxn];

int gcd(int a, int b) {
	return b==0?a:gcd(b, a%b);
}

void init() {
	memset(dp, 0, sizeof(dp));	
	memset(ans, 0, sizeof(ans));

	for (int i = 1; i <= 300; i++)
		for (int j = 1; j <= 300; j++)
			dp[i][j] = dp[i-1][j] + dp[i][j-1] - dp[i-1][j-1] + (gcd(i, j) == 1);

	for (int i = 1; i <= 300; i++)
		for (int j = 1; j <= 300; j++)
			ans[i][j] = ans[i-1][j] + ans[i][j-1] - ans[i-1][j-1] + dp[i][j] - dp[i>>1][j>>1];
}

int main() {
	init();
	while (scanf("%d%d", &n, &m) != EOF && n+m) {
		printf("%lld\n", ans[n-1][m-1] * 2);	
	}
	return 0;
}