POJ 1692 Crossed Matchings（DP)

POJ 1692 Crossed Matchings（DP)

Description

There are two rows of positive integer numbers. We can draw one line segment between any two equal numbers, with values r, if one of them is located in the first row and the other one is located in the second row. We call this line segment an r-matching segment. The following figure shows a 3-matching and a 2-matching segment.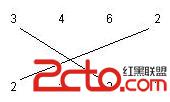

We want to find the maximum number of matching segments possible to draw fZ喎?http://www.Bkjia.com/kf/ware/vc/" target="_blank" class="keylink">vciB0aGUgZ2l2ZW4gaW5wdXQsIHN1Y2ggdGhhdDogPGJyPgoxLiBFYWNoIGEtbWF0Y2hpbmcgc2VnbWVudCBzaG91bGQgY3Jvc3MgZXhhY3RseSBvbmUgYi1tYXRjaGluZyBzZWdtZW50LCB3aGVyZSBhICE9IGIgLiA8YnI+CjIuIE5vIHR3byBtYXRjaGluZyBzZWdtZW50cyBjYW4gYmUgZHJhd24gZnJvbSBhIG51bWJlci4gRm9yIGV4YW1wbGUsIHRoZSBmb2xsb3dpbmcgbWF0Y2hpbmdzIGFyZSBub3QgYWxsb3dlZC4gPGJyPgo8Y2VudGVyPjxpbWcgc3JjPQ=="http://www.2cto.com/uploadfile/Collfiles/20140817/20140817093606172.jpg" alt="\">
Write a program to compute the maximum number of matching segments for the input data. Note that this number is always even.

Input

The first line of the input is the number M, which is the number of test cases (1 <= M <= 10). Each test case has three lines. The first line contains N1 and N2, the number of integers on the first and the second row respectively. The next line contains N1 integers which are the numbers on the first row. The third line contains N2 integers which are the numbers on the second row. All numbers are positive integers less than 100.

Output

Output should have one separate line for each test case. The maximum number of matching segments for each test case should be written in one separate line.

Sample Input

3
6 6
1 3 1 3 1 3
3 1 3 1 3 1
4 4
1 1 3 3 
1 1 3 3 
12 11
1 2 3 3 2 4 1 5 1 3 5 10
3 1 2 3 2 4 12 1 5 5 3 

Sample Output

6
0
8

題意：相同數字可以連接但是必須和不同數字的連接交叉。問最大可能性

dp[i][j]表示第一行的前i個和第二行的前j個的最大可能。

#include
using namespace std;
int a[110],b[110];
int dp[110][110];
int n,m,t;

int main()
{
    int k1,k2;
    scanf("%d",&t);
    while(t--)
    {
        scanf("%d%d",&n,&m);
        for(int i=1;i<=n;i++)
            scanf("%d",&a[i]);
        for(int j=1;j<=m;j++)
            scanf("%d",&b[j]);
        memset(dp,0,sizeof(dp));
        for(int i=2;i<=n;i++)
        {
            for(int j=2;j<=m;j++)
            {
                dp[i][j]=max(dp[i-1][j],dp[i][j-1]);//相等時可達到的dp[i][j]的狀態的最大值
                if(a[i]!=b[j])
                {
                    for(k1=i;k1>=1;k1--)
                    {
                        if(b[j]==a[k1])
                            break;
                    }
                    for(k2=j;k2>=1;k2--)
                    {
                        if(a[i]==b[k2])
                            break;
                    }
                    if(k1&&k2)
                        dp[i][j]=max(dp[i][j],dp[k1-1][k2-1]+2);//更新dp[i][j]
                }
            }
        }
        printf("%d\n",dp[n][m]);
    }
    return 0;
}