poj2528--Mayor's posters(線段樹+離散化)

poj2528--Mayor's posters(線段樹+離散化)

Mayor's posters Time Limit: 1000MS Memory Limit: 65536K Total Submissions: 41785 Accepted: 12164

Description

The citizens of Bytetown, AB, could not stand that the candidates in the mayoral election campaign have been placing their electoral posters at all places at their whim. The city council has finally decided to build an electoral wall for placing the posters and introduce the following rules:
Every candidate can place exactly one poster on the wall.
All posters are of the same height equal to the height of the wall; the width of a poster can be any integer number of bytes (byte is the unit of length in Bytetown).
The wall is divided into segments and the width of each segment is one byte.
Each poster must completely cover a contiguous number of wall segments.
They have built a wall 10000000 bytes long (such that there is enough place for all candidates). When the electoral campaign was restarted, the candidates were placing their posters on the wall and their posters differed widely in width. Moreover, the candidates started placing their posters on wall segments already occupied by other posters. Everyone in Bytetown was curious whose posters will be visible (entirely or in part) on the last day before elections.
Your task is to find the number of visible posters when all the posters are placed given the information about posters' size, their place and order of placement on the electoral wall.

Input

The first line of input contains a number c giving the number of cases that follow. The first line of data for a single case contains number 1 <= n <= 10000. The subsequent n lines describe the posters in the order in which they were placed. The i-th line among the n lines contains two integer numbers l_i and ri which are the number of the wall segment occupied by the left end and the right end of the i-th poster, respectively. We know that for each 1 <= i <= n, 1 <= l_i <= ri <= 10000000. After the i-th poster is placed, it entirely covers all wall segments numbered l_i, l_i+1 ,... , ri.

Output

For each input data set print the number of visible posters after all the posters are placed.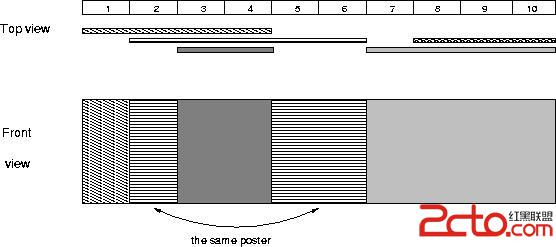

The picture below illustrates the case of the sample input.

Sample Input

1
5
1 4
2 6
8 10
3 4
7 10

Sample Output

4

題意：給出一面牆，給出n張海報貼在牆上，每張海報都覆蓋一個范圍，問最後可以看到多少張海報

海報覆蓋的范圍很大，直接使用數組存不下，但是只有最多10000張海報，也就是說最多出現20000個點，所以可以使用離散化，將每個點離散後，重新對給出控制的區間，這樣區間最大就是1到20000.可以直接使用線段樹，成段更新，每次更新一個顏色，最後遍歷所有的段，將還可以遍歷的顏色儲存，統計

將-1 定義為沒有顏色，0代表有多種顏色，1到m代表各自的顏色，線段樹只要在0時向下深入，其他的直接統計顏色。

但是這個題中的離散化有問題，會擠掉中間的顏色，不過poj好像也是這麼做的，沒有考慮中間的顏色。

如 1 ，10 1，4 7,10 這三組數的正確結果應該是還可以看到3種顏色，但是如果直接排列點的話就會擠掉5到6這一種顏色。

真正的這種成段的離散化，一定要將兩個節點中還有值的話，要多加一個節點，代表兩個節點中間的值。

#include 
#include 
#include 
using namespace std;
#define maxn 30000
#define lmin 1
#define rmax n
#define lson l,(l+r)/2,rt<<1
#define rson (l+r)/2+1,r,rt<<1|1
#define root lmin,rmax,1
#define now l,r,rt
#define int_now int l,int r,int rt
int cl[maxn<<2] , lazy[maxn<<2] , a[maxn] ;
struct node{
    int id1 , id2 , k ;
}p[maxn];
bool cmp(node a,node b)
{
    return a.k < b.k ;
}
void push_up(int_now)
{
    if( !cl[rt<<1] || !cl[rt<<1|1] || cl[rt<<1] != cl[rt<<1|1] )
        cl[rt] = 0 ;
    else
        cl[rt] = cl[rt<<1|1] ;
}
void push_down(int_now)
{
    if( lazy[rt] != -1 )
    {
        lazy[rt<<1] = lazy[rt<<1|1] = lazy[rt] ;
        cl[rt<<1] = cl[rt<<1|1] = lazy[rt] ;
        lazy[rt] = -1 ;
    }
}
void update(int ll,int rr,int x,int_now)
{
    if( ll > r || rr < l )
        return ;
    if( ll <= l && r <= rr )
    {
        cl[rt] = lazy[rt] = x ;
        return ;
    }
    push_down(now);
    update(ll,rr,x,lson);
    update(ll,rr,x,rson);
    push_up(now);
}
void query(int ll,int rr,int_now,int *a)
{
    if( cl[rt] == -1 )
        return ;
    else if(cl[rt] > 0)
    {
        a[ cl[rt] ] = 1 ;
        return ;
    }
    push_down(now);
    query(ll,rr,lson,a);
    query(ll,rr,rson,a);
}
int main()
{
    int t , i , n , m , l , r , x ;
    scanf("%d", &t);
    while(t--)
    {
        scanf("%d", &m);
        for(i = 0 ; i < m ; i++)
        {
            scanf("%d %d", &p[i].k, &p[i+m].k);
            p[i].id1 = i ;
            p[i+m].id1 = i+m ;
        }
        sort(p,p+2*m,cmp);
        int temp = -1 ;
        n = 0 ;
        for(i = 0 ; i < 2*m ; i++)
        {
            if( p[i].k == temp )
                p[i].id2 = n ;
            else
            {
                p[i].id2 = ++n ;
                temp = p[i].k ;
            }
            a[ p[i].id1 ] = p[i].id2 ;
        }
        memset(cl,-1,sizeof(cl));
        memset(lazy,-1,sizeof(lazy));
        for(i = 0 ; i < m ; i++)
        {
            update(a[i],a[i+m],i+1,root);
        }
        memset(a,0,sizeof(a));
        query(1,n,root,a);
        int num = 0;
        for(i = 1 ; i <= m ; i++)
            if(a[i])
                num++ ;
        printf("%d\n", num);
    }
    return 0;
}