篩選素數方法小結:
最簡單的篩素數法方法就是從2開始,將所以2的倍數去掉,然後從3開始,將3的倍數去掉,依次進行下去即可。根據這樣很容易寫出代碼,下面代碼就是是篩素數法得到100以內的素數並保存到primes[]數組中。

1 const int MAXN = 100;
2 bool flag[MAXN];
3 int primes[MAXN / 3], pi;
4 void GetPrime_1()
5 {
6 int i, j;
7 pi = 0;
8 memset(flag, false, sizeof(flag));
9 for (i = 2; i < MAXN; i++)
10 if (!flag[i])
11 {
12 primes[pi++] = i;
13 for (j = i; j < MAXN; j += i) //剔除待考察數據j的倍數,並置其flag位為true
14 flag[j] = true;
15 }
16 }

可以看出這種會有很多重復訪問,如在訪問flag[2]和flag[5]時會各訪問flag[10]一次。因此最好想方法來減少這種重復訪問,讓flag[]數組的每個元素只被訪問一次。可以這樣考慮——簡單的篩素數法是利用一個素數的倍數必須不是素數,同樣任何一個數與其它所有素數的乘積必然也不是素數(這是因為每個合數必有一個最小素因子)。
為了試驗這種想法,先用2到10之間的數來驗證下。
2,3,4,5,6,7,8,9,10 初始時所以flag都是無標記的。
第一步 訪問2,flag[2]無標記所以將2加入素數表中,然後將2與素數表中的所有數相乘得到的數必定不是素數,2*2=4因此標記flag[4]。
2,3,4,5,6,7,8,9,10
第二步 訪問3,flag[3]無標記所以將3加入素數表中,將3與素數表中的所有數相乘得到的數必定不是素數,3*2=6,3*3=9因此標記flag[6]和flag[9]。
2,3,4,5,6,7,8,9,10
第三步 訪問4,flag[4]有標記所以4不加入素數表中,將4與素數表中的所有數相乘得到的數必定不是素數, 4*2=8,4*3=12因此標記flag[8]。
2,3,4,5,6,7,8,9,10
第四步 訪問5,flag[5]無標記所以將5加入素數表中,將5與素數表中的所有數相乘得到的數必定不是素數,5*2=10,5*3=15因此標記flag[10]。
2,3,4,5,6,7,8,9,10
第五步 訪問6,flag[6]有標記所以6不加入素數表中,將6與素數表中的所有數相乘得到的數必定不是素數, 6*2=12,6*3=18,6*5=30。
2,3,4,5,6,7,8,9,10
後面幾步類似,具體代碼如下:

1 const int MAXN = 100;
2 bool flag[MAXN];
3 int primes[MAXN / 3], pi;
4 void GetPrime_2()
5 {
6 int i, j;
7 pi = 0;
8 memset(flag, false, sizeof(flag));
9 for (i = 2; i < MAXN; i++)
10 {
11 if (!flag[i])
12 primes[pi++] = i; //flag未標記為true,將其加入到素數表中
13 for (j = 0; (j < pi) && (i * primes[j] < MAXN); j++) //依次剔除待考察數據與素數表中數據的乘積,並置其flag位為true
14 flag[i * primes[j]] = true;
15 }
16 }

這份代碼對不對呢?仔細回顧下分析過程,可以發現有些數據還是被訪問了多次,這當然不是我們希望的結果,我們的要求是讓每個合數僅被它的最小素因子篩去一次。比如12,它的最小素因子是2,所以就只應該被在計算6*2時去訪問,而且不應該在計算4*3時去訪問,同理18也只應該被在計算9*2時去訪問,而且不應該在計算6*3時去訪問。
找到原因後,再來思考如何解決。6*3不行而9*2可以了,是因為6是2的倍數,所以在計算6*2之後就不能再將6與比2大的素數相乘,這些相乘的結果必定會導致重復計算。因此對於任何數來說,如果它是該素數的倍數那麼它就不能再與素數表中該素數之後的素數相乘了,如9是3的倍數,所以在9*3之後就不能再去用計算9*5了。因此在代碼中再增加一行判斷語句:

1 const int MAXN = 100;
2 bool flag[MAXN];
3 int primes[MAXN / 3], pi;
4 void GetPrime_2()
5 {
6 int i, j;
7 pi = 0;
8 memset(flag, false, sizeof(flag));
9 for (i = 2; i < MAXN; i++)
10 {
11 if (!flag[i])
12 primes[pi++] = i;
13 for (j = 0; (j < pi) && (i * primes[j] < MAXN); j++)
14 {
15 flag[i * primes[j]] = true;
16 if (i % primes[j] == 0) //這句保證每個非素數只被篩去一次
17 break;
18 }
19 }
20 }

想知道這二種篩素數法方法的區別嗎?現在對求2到1億之間的素數進行測試,看看區別到底會有多大,測試代碼如下:

1 /*
2 *描述:篩素數法(倍數剔除、最小素因子篩選)對比
3 *分析:倍數剔除:一個素數的倍數必須不是素數,即從2開始,將所以2的倍數去掉,然後從3開始,將3的倍數去掉,依次進行下去即可
4 * 最小素因子篩選:簡單的篩素數法(倍數剔除)是利用一個素數的倍數必須不是素數,同樣任何一個數與其它所有素數的乘積必然也不是素數(這是因為每個合數必有一個最小素因子)。
5 要求是讓每個合數僅被它的最小素因子篩去一次;即如果它是該素數的倍數那麼它就不能再與素數表中該素數之後的素數相乘了。
6 *
7 *
8 */
9 #include <stdio.h>
10 #include <stdlib.h>
11 #include <memory.h>
12 #include <time.h>
13 #include <math.h>
14 const int MAXN = 100000000;
15 bool flag[MAXN];
16 int primes[MAXN / 3], pi;
17 // 利用對每個素數的倍數必定不是素數來篩選
18 void GetPrime_1()
19 {
20 int i, j;
21 pi = 0;
22 memset(flag, false, sizeof(flag));
23 for (i = 2; i < MAXN; i++)
24 if (!flag[i])
25 {
26 primes[pi++] = i;
27 for (j = i; j < MAXN; j += i)
28 flag[j] = true;
29 }
30 }
31 // 利用了每個合數必有一個最小素因子來篩選
32 void GetPrime_2()
33 {
34 int i, j;
35 pi = 0;
36 memset(flag, false, sizeof(flag));
37 for (i = 2; i < MAXN; i++)
38 {
39 if (!flag[i])
40 primes[pi++] = i;
41 for (j = 0; (j < pi) && (i * primes[j] < MAXN); j++)
42 {
43 flag[i * primes[j]] = true;
44 if (i % primes[j] == 0)
45 break;
46 }
47 }
48 }
49 int main()
50 {
51 printf(" 在%d的數據量下普通的篩素數方法與改進之後的效率對比\n", MAXN);
52 clock_t clockBegin, clockEnd;
53
54 clockBegin = clock();
55 GetPrime_1();
56 clockEnd = clock();
57 printf("普通的篩素數方法\t%d毫秒\n", clockEnd - clockBegin);
58
59 clockBegin = clock();
60 GetPrime_2();
61 clockEnd = clock();
62 printf("改進的篩素數方法\t%d毫秒\n", clockEnd - clockBegin);
63 system("pause");
64 return 0;
65 }

具體的運行結果如下:
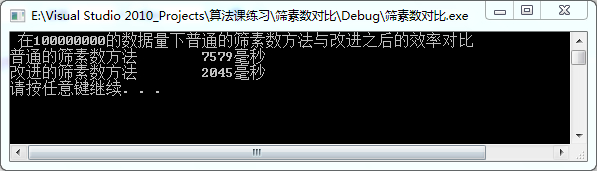
總結:
1.普通的篩素數的原理是一個素數的倍數必須不是素數。
2.改進的篩素數的原理是每個合數必有一個最小素因子,根據每個最小素因子去訪問合數就能防止合數被重復訪問。
我是天王蓋地虎的分割線
參考:http://www.cnblogs.com/xymqx/p/3718276.html
#include <iostream>
using namespace std;
void FilterPrime(int n)
{
bool* isPrimes = new bool[n+1]; //判斷是否為素數的數組
for(int i=2;i<=n;++i) //將每一位都初始化為是素數
{
isPrimes[i] = true;
}
isPrimes[2] = true; //2為素數
for(int j=2;j<=n;++j)
{
if(isPrimes[j]==true) //如果j為素數,則它的倍數都不是素數
{
for(int m=2;j*m<=n;++m) //它的倍數都不是素數
{
isPrimes[j*m] = false;
}
}
}
for(int k=2;k<=n;++k)
{
if(isPrimes[k]==true)
{
cout<<k<<"是素數"<<endl;
}
}
delete [] isPrimes; //刪除;
}
int main()
{
int num;
cin>>num;
FilterPrime(num);
system("pause");
return 0;
}
主要問題出在erat_sieve函數的n=n/2;這個語句上了,本來要計算的是200。結果你在這裡把n折半,結果就再後面m=sqrt(n);m的取值就不是根號下200而是100結果10以上的素數就沒有做為因子用上,所以直接導致121和169沒有被清除出來。
你這個方法不是篩法吧,篩法是不用除法了求模運算的。我寫個篩法你看看
#include "stdio.h"
#include "math.h"
int main()
{
char prime[10000]={0};
int i,j,n,m;
for(i=3;i<10000;i+=2) prime[i]=1;
prime[2]=1;
printf("輸入整數n(1~n):");
scanf("%d",&n);
m=sqrt(n);
for(i=3;i<m;i++)
{
for(j=i*2;j<n;j+=i)
{
if(prime[j]) prime[j]=0;
}
}
j=0;
for(i=0;i<n;i++)
{
if(prime[i])
{
printf("%3d ",i);
j++;
if(j%10==0) printf("\n");
}
}
printf("\n%3d ",j);
}