2.11 2D平面最近點對問題[closest pair problem],closestpair
【本文鏈接】
http://www.cnblogs.com/hellogiser/p/closest-pair-problem.html
【題目】
給定平面上N個點的坐標,找出距離最近的兩個點之間的距離。
【蠻力法】
對於n個點,一共可以組成n(n-1)/2對點對,對這n(n-1)/2對點對逐對進行距離計算,通過循環求得點集中的最近點對。時間復雜度為T(n)=n^2。
C++ Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
/*
version: 1.0
author: hellogiser
blog: http://www.cnblogs.com/hellogiser
date: 2014/7/11
*/
struct Point
{
double x;
double y;
}
double distance(const Point &a, const Point &b) const
{
// distance of point a and b
return sqrt((a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y));
}
double ClosestPairBruteforce(Point P[], int n)
{
// O(n^2)
// input: a list P of n points
// output: distance of the closest pair of points
double dmin = DBL_MAX;
int i, j;
for (i = 0; i < n; i++)
for( j = i + 1; j < n; j++)
{
d = distance(P[i], P[j]);
if (d < dmin)
{
dmin = d;
}
}
return dmin;
}
【分治法】
首先劃分集合S為SL和SR,使得SL中的每一個點位於SR中每一個點的左邊,並且SL和SR中點數相同。分別在SL和SR中解決最近點對問題,得到d1和d2,分別表示SL和SR中的最近點對的距離。令d=min(d1,d2)。如果S中的最近點對(p,q),p在SL並且q在SR中,那麼p和q一定在以L為中心的帶狀區域內,以L-d和L+d為界,如下圖所示:
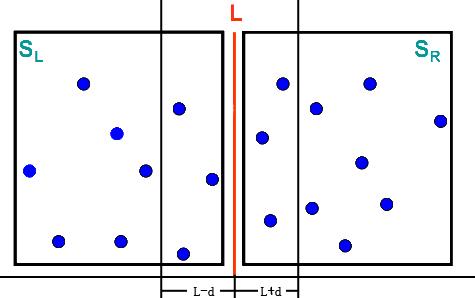
可以證明,對於[L-d,L]區域中的p點,在[L,L+d]中至多需要計算與6個點之間的距離。(證明略)
思路如下
Pseudo Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
/*
version: 1.0
author: hellogiser
blog: http://www.cnblogs.com/hellogiser
date: 2014/7/11
*/
ClosestPair(S)
if S.size=1 return DBL_MAX
if S.size2=2 return distance(S[0],S[1])
//otherwise,do the following
let L = median(S)
divide S into SL and SR at L
d1 = CloestPair(SL)
d2 = CloestPair(SR)
d12 = CrossPair(SL,SR)
return min(d1,d2,d12)
時間復雜度為T(n)=2T(n/2)+(n/2)*6,可以得到時間復雜度為O(nlgn)。
具體步驟如下:
Step 0 Sort the points by x (list one) and then by y (list two).
Step 1 Divide the points given into two subsets S1 and S2 by a vertical line
x =
m so that half the points lie to the left and half the points lie to the right.
(Note: set m = (x[N/2]+x[N/2+1])/2 so that no points lie on the split line.)
Step 2 Find recursively the closest pairs for the left and right subsets.
Step 3 Set
d = min{
d1,
d2}
We can limit our attention to the points in the symmetric vertical strip of width 2
d as possible closest pair. Let C1 and C2 be the subsets of points in the left subset S1 and of the right subset S2, respectively, that lie in this vertical strip. The points in C1 and C2 are stored in increasing order of their y coordinates, taken from the second list.
Step 4 For every point
P(
x,
y) in C1, we inspect points in C2 that may be closer to
P than
d. There can be no more than 6 such points (because
d ≤
d2)!
偽代碼如下:
Pseudo Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
/*
version: 1.0
author: hellogiser
blog: http://www.cnblogs.com/hellogiser
date: 2014/7/11
*/
GetCloestPair(pts, n)
copy pts[0..n-1] to ptsByX[0..n-1],ptsByY[0..n-1]
qsort(ptsByX,cmpX)
qsort(ptsByY,cmpY)
ClosestPair(ptsByX, ptsByY, n)
ClosestPair(ptsByX, ptsByY, n)
// Base cases
if (n = 1) return INT_MAX
if (n = 2) return distance(ptsByX[0], ptsByX[1])
// Divide S into SL SR by line x = xm
mid = n/2 -1
copy ptsByX[0 . . . mid] into new array XL in x order
copy ptsByX[mid+1 . . . n−1] into new array XR
copy ptsByY[0 . . . mid] into new array YL in y order
copy ptsByY[mid+1 . . . n−1] into new array YR
// XL and YL refer to same points, as do XR,YR.
// Conquer
d1 = ClosestPair(XL, YL, floor(n/2))
d2 = ClosestPair(XR, YR, ceil(n/2))
// Combine sub solutions to final solution
d12 = CrossPair(ptsByX,XL,XR,n,d1,d2);
return min(d1,d2,d12)
其中最為重要的是CrossPair步驟。
Pseudo Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
CrossPair(ptsByX,XL,XR,n,d1,d2)
mid = n/2 -1
d = min(d1, d2)
xm = (ptsByX[mid]+ptsByX[mid+1])/2
//C1: Select points in XL where x>xm-d
i = mid
while(i>=0&&XL[i].x>xm-d)
add XL[i] to C1
i = i-1
//C1=XL[i+1..mid]
//C2: Select points in XR where x<xm+d
j = mid+1
while(j<=n-1&&XR[j].x<xm+d)
add XR[j] to C2
j = j+1
//C2=XL[mid+1..j-1]
// For given Point P in C1, there are at most 6 points in C2 within distance of d
minDist = DBL_MAX
for(i=0;i<C1.length;i++)
p = C1[i]
for(j=0;j<C2.length;j++)
q = C2[j]
// Make sure Q within d*2d rectangel of P(at most 6 Q)
if(p.y-d<q.y<p.y+d)
dist = distance(p,q)
if(minDist>dist)
minDist = dist
return minDist
可以通過left和right下標來表示C1和C2,這樣可以進一步優化為
Pseudo Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
CrossPair(ptsByX,XL,XR,n,d1,d2)
mid = n/2 -1
d = min(d1, d2)
xm = (ptsByX[mid]+ptsByX[mid+1])/2
//C1: Select points in XL where x>xm-d
i = mid
while(i>=0&&XL[i].x>xm-d)
i = i-1
left = i+1
//C1=XL[left..mid]
//C2: Select points in XR where x<xm+d
j = mid+1
while(j<=n-1&&XR[j].x<xm+d)
j = j+1
right = j-1
//C2=XL[mid+1..right]
// For given Point P in C1, there are at most 6 points in C2 within distance of d
minDist = DBL_MAX
for(i=left;i<=mid;i++)
p = XL[i]
for(j=mid+1;j<=right;j++)
q = XR[j]
// Make sure Q within d*2d rectangel of P(at most 6 Q)
if(p.y-d<q.y<p.y+d)
dist = distance(p,q)
if(minDist>dist)
minDist = dist
return minDist
【參考】
http://blog.csdn.net/junerfsoft/article/details/2975495
http://blog.csdn.net/midgard/article/details/4199043
http://www.cnblogs.com/AdaByron/archive/2011/10/07/2200966.html
http://www.cnblogs.com/pangxiaodong/archive/2011/09/30/2196684.html
【本文鏈接】
http://www.cnblogs.com/hellogiser/p/closest-pair-problem.html
ACM:給定點集S,S中周長最小的三角形(點集中點數N<=20000),一個復雜度可接受的算法(n^2以下)
用分治就可以過了。樓主可以參考一下最近點對問題的算法:
en.wikipedia.org/...roblem
算法如下:先將所有的點按x坐標排序,然後每次分成左右兩個部分,分別遞歸求解這兩個點集中的最小周長。最後考慮跨越這兩個點集的3個點的最小周長,用當前求得的最優解可以縮小枚舉的范圍。
