一、前言
最短路徑算法,顧名思義就是求解某點到某點的最短的距離、消耗、費用等等,有各種各樣的描述,在地圖上看,可以說是圖上一個地點到達另外一個地點的最短的距離。比方說,我們把地圖上的每一個城市想象成一個點,從一個城市到另一個城市的花費是不一樣的。現在我們要從上海去往北京,需要考慮的是找到一條路線,使得從上海到北京的花費最小。有人可能首先會想到,飛機直達啊,這當然是時間消耗最小的方法,但是考慮到費用的高昂,這條線路甚至還不如上海到北京的高鐵可取。更有甚者,假設國家開通了從上海到西藏,再從西藏到蘭州等等城市經過萬般周折最後到達北京的一條線路,雖然要需要經歷較長一段時間,但是價錢相比前二者非常實惠(假設只要一塊錢,便能跑大半個中國,領略多省風光),單從省錢的角度看來,自然最後這條是可取的。這就是我們在這裡所說的單源最短路徑。我們接下來的篇幅中將去講解所有邊權值為非負的有向圖的單源最短路徑,由於無向圖相當於變相的有向圖,在這裡就不做解釋,留作讀者自行推廣。
二、概念
這裡我們講解最短路徑,需要掌握幾個基本的概念:
對於有向圖G=(V,E),權值函數W: E→R(即每條邊的權值都為一個實數)
1、路徑
三、最優子結構
我們不難發現,求解源點到某一頂點的最短路徑,其實不比求解源點到所有頂點的路徑簡單。這個時候我們要引入全局的概念,能不能找出所有的頂點的最短路徑,然後再去查看到目標點的最短路徑呢?很多人就會想到動態規劃這一思想,說道動態規劃,自然我們首先要考慮的問題是最優子結構。
最短路徑滿足最優子結構性質:最短路徑的子路徑是最短路徑。
證明:(剪貼法)

前提:u到v是最短路徑。
假設:x到y不是最短路徑,那麼存在一條更短的路徑從x到y(假設為下面的彎箭頭),這樣,刪去原路徑中從x到y的路徑,用新找到的路徑替代(彎箭頭),那麼就得到 了一條比u到v的權值更短的路徑,這與前提u到v是最短路徑相矛盾,因而x到y是最短路徑,即最短路徑滿足最優子結構性質。
引入三角不等式的概念:(從u到v的最短路徑權值,小於等於從u到x的最短路徑權值加上從x到v的最短路徑權值)
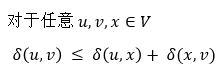
這個性質根據最優子結構性質而來,非常重要。
四、單元最短路徑問題
對於圖G= (V, E),給定源點s,找到從s到所有頂點v的最短路徑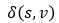 。
。
由於在本文中我們講解Dijkstra算法,需要假設沒有負權值,即:
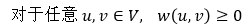
因而,只要路徑存在,便存在最短路徑。
五、Dijkstra算法思想
Dijkstra是非常非常著名的計算機科學家,可能很多人對他的了解只在他的單元最短路徑算法上,對操作系統了解的人可能還了解他的銀行家算法,在方法學領域還有goto有害論等等。當然要講他的其他傑出貢獻,那就要把話題扯遠了,今天我們只講講Dijkstra算法的思想,然後在後面給出它的實現過程,必要的給出其正確性的證明(Dijkstra在程序正確性證明領域發明了最弱前置謂詞證明方法,不過我們不會用他的方法證明他老人家的程序的正確性,不然就扯到了十萬八千裡-。-)。
算法思想:
(1)在任意時刻,我們都要得到從源點到所有頂點的估算距離,並維持一個頂點集合S,若頂點v在S中,則說明從源點到v的最短路徑已知;
(2)在每一次將不在S中的頂點v加到S中去時,總是選擇從源點到v的估算距離最小的;
(3)頂點v加入S中之後,對於所有與v相鄰的頂點(不屬於S),更新它們的估算距離。
由(2),我們看到了貪心的影子,在每次選擇時,我們總是想選擇花費最小的,正常人都會這樣去想,至於為什麼這樣選,這樣選對不對,我們將在後面進行證明。
偽代碼如下:
1 Dijkstra(G, W, s) //G表示圖,W表示權值函數,s表示源頂點
2 d[s] ←0 //源點到源點最短路為0
3 for each v ∈ V - {s} //3-8行均為初始化操作
4 do d[v]←∞
5 parent[v]←NIL
6 S←∅
7 Q←V //此處Q為優先隊列,存儲未進入S的各頂點以及從源點到這些頂點的估算距離,采用二叉堆(最小堆)實現,越小越優先
8 while Q≠∅
9 do u←Extract-Min(Q) //提取估算距離最小的頂點,在優先隊列中位於頂部,出隊列,放入集合S中
10 S←S∪{u}
11 for each v ∈ Adj(u) //松弛操作,對與u相鄰的每個頂點v,進行維持三角不等式成立的松弛操作。
12 do if d[v] > d[u] + w(u, v)
13 then d[v] = d[u] + w(u, v) //這一步隱含了更新優先隊列中的值,DECREASE。
14 parent[v]←u //置v的前驅結點為u
六、簡單例子說明
初始情況:
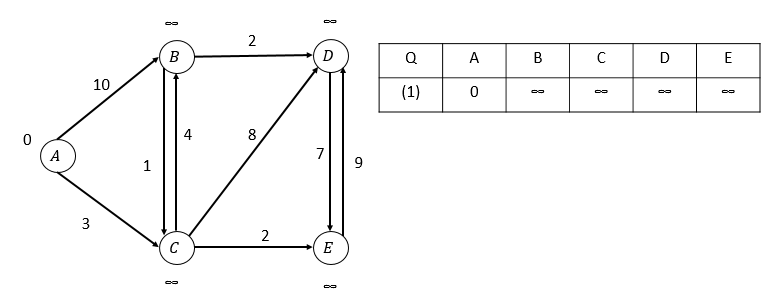
第一次松弛,選取A頂點:
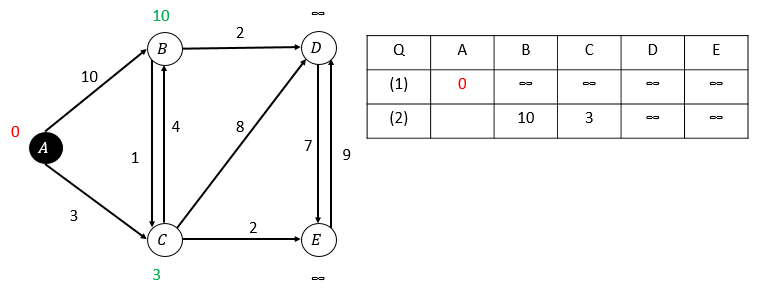
第二次松弛,C的估算距離最小,選取C頂點:
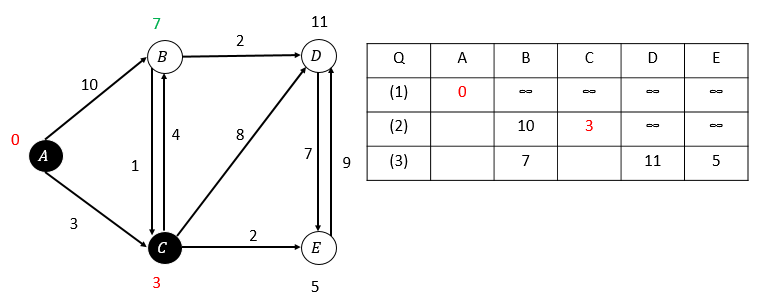
第三次松弛,E的估算距離最小,選取E:
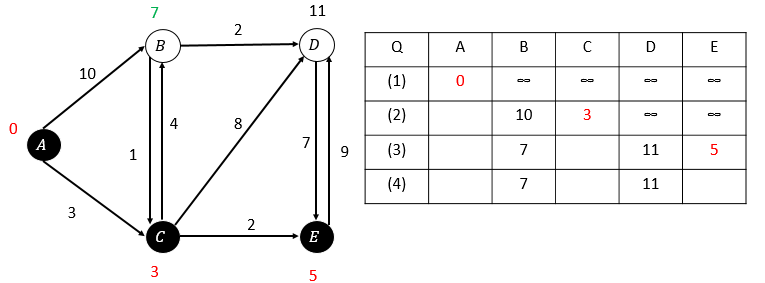
第四次松弛,B的估算距離最小,選取B:
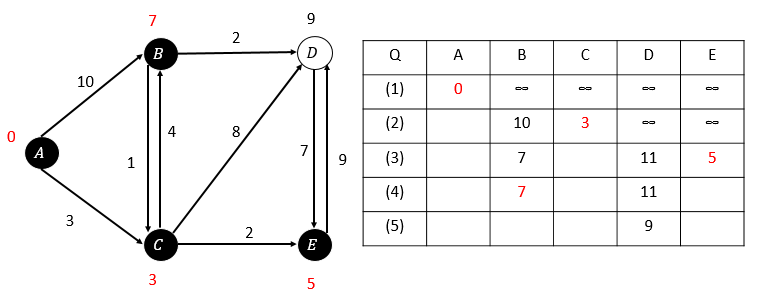
第五次松弛:(最後一個點,完成)
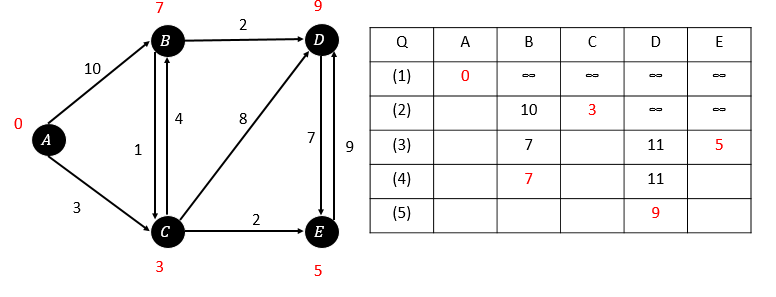
經過所有的松弛操作之後,我們就得到了所有頂點的最短路徑(表格中紅字部分)。
如果加上對parent[]進行的操作,我們還可以得到一棵最短路徑樹,這個讀者可以自行推廣。
七、代碼實現
相比正確性,可能大家更加關注的是代碼的實現,這裡我們給出Dijkstra的實現代碼,圖結構的存儲采用鄰接矩陣和鄰接表兩種形式,有關圖的表示方法,可以參看下面的博客:http://www.cnblogs.com/dzkang2011/p/graph_1.html。優先隊列采用C++ 優先隊列STL,priority_queue,由於無法直接更改隊列中的值,我們需要對實現進行稍微的修改,這對最後結果不會產生影響,詳情見代碼。
1、鄰接表C/C++:
1 #include <iostream>
2 #include <cstdio>
3 #include <vector>
4 #include <queue>
5 using namespace std;
6
7 #define maxn 110 //最大頂點個數
8 int n; //頂點個數
9
10 struct arcnode //邊結點
11 {
12 int vertex; //與表頭結點相鄰的頂點編號
13 int weight; //連接兩頂點的邊的權值
14 arcnode * next; //指向下一相鄰接點
15 arcnode() {}
16 arcnode(int v,int w):vertex(v),weight(w),next(NULL) {}
17 };
18
19 struct vernode //頂點結點,為每一條鄰接表的表頭結點
20 {
21 int vex; //當前定點編號
22 arcnode * firarc; //與該頂點相連的第一個頂點組成的邊
23 }Ver[maxn];
24
25 void Init() //建立圖的鄰接表需要先初始化,建立頂點結點
26 {
27 for(int i = 1; i <= n; i++)
28 {
29 Ver[i].vex = i;
30 Ver[i].firarc = NULL;
31 }
32 }
33
34 void Insert(int a, int b, int w) //尾插法,插入以a為起點,b為終點,權為w的邊,效率不如頭插,但是可以去重邊
35 {
36 arcnode * q = new arcnode(b, w);
37 if(Ver[a].firarc == NULL)
38 Ver[a].firarc = q;
39 else
40 {
41 arcnode * p = Ver[a].firarc;
42 if(p->vertex == b)
43 {
44 if(p->weight > w)
45 p->weight = w;
46 return ;
47 }
48 while(p->next != NULL)
49 {
50 if(p->next->vertex == b)
51 {
52 if(p->next->weight > w);
53 p->next->weight = w;
54 return ;
55 }
56 p = p->next;
57 }
58 p->next = q;
59 }
60 }
61 void Insert2(int a, int b, int w) //頭插法,效率更高,但不能去重邊
62 {
63 arcnode * q = new arcnode(b, w);
64 if(Ver[a].firarc == NULL)
65 Ver[a].firarc = q;
66 else
67 {
68 arcnode * p = Ver[a].firarc;
69 q->next = p;
70 Ver[a].firarc = q;
71 }
72 }
73 struct node //頂點節點,保存id和到源頂點的估算距離,優先隊列需要的類型
74 {
75 int id; //源頂點id和估算距離
76 int w;
77 friend bool operator<(node a, node b) //因要實現最小堆,按升序排列,因而需要重載運算符,重定義優先級,以小為先
78 {
79 return a.w > b.w;
80 }
81 };
82
83 #define INF 0xfffff //權值上限
84 int parent[maxn]; //每個頂點的父親節點,可以用於還原最短路徑樹
85 bool visited[maxn]; //用於判斷頂點是否已經在最短路徑樹中,或者說是否已找到最短路徑
86 node d[maxn]; //源點到每個頂點估算距離,最後結果為源點到所有頂點的最短路。
87 priority_queue<node> q; //優先隊列stl實現
88 void Dijkstra(int s) //Dijkstra算法,傳入源頂點
89 {
90 for(int i = 1; i <= n; i++) //初始化
91 {
92 d[i].id = i;
93 d[i].w = INF; //估算距離置INF
94 parent[i] = -1; //每個頂點都無父親節點
95 visited[i] = false; //都未找到最短路
96 }
97 d[s].w = 0; //源點到源點最短路權值為0
98 q.push(d[s]); //壓入隊列中
99 while(!q.empty()) //算法的核心,隊列空說明完成了操作
100 {
101 node cd = q.top(); //取最小估算距離頂點
102 q.pop();
103 int u = cd.id;
104 if(visited[u]) //注意這一句的深意,避免很多不必要的操作
105 continue;
106 visited[u] = true;
107 arcnode * p = Ver[u].firarc;
108 //松弛操作
109 while(p != NULL) //找所有與他相鄰的頂點,進行松弛操作,更新估算距離,壓入隊列。
110 {
111 int v = p->vertex;
112 if(!visited[v] && d[v].w > d[u].w+p->weight)
113 {
114 d[v].w = d[u].w+p->weight;
115 parent[v] = u;
116 q.push(d[v]);
117 }
118 p = p->next;
119 }
120 }
121 }
122
123 int main()
124 {
125 int m, a, b, c, st, ed;
126 printf("請輸入頂點數和邊數:\n");
127 scanf("%d%d", &n, &m);
128 printf("請輸入邊以及權值(a, b, c)\n");
129 Init(); //計算前必須初始化
130 while(m--)
131 {
132 scanf("%d%d%d", &a, &b, &c);
133 Insert2(a, b, c); //無向圖注意存儲兩條邊
134 Insert2(b, a, c);
135 }
136 printf("請輸入起點和終點:\n");
137 scanf("%d%d", &st, &ed);
138 Dijkstra(st);
139 if(d[ed].w != INF)
140 printf("最短路徑權值為:%d\n", d[ed].w);
141 else
142 printf("不存在從頂點%d到頂點%d的最短路徑。\n", st, ed);
143 return 0;
144 }
2、鄰接矩陣C/C++:
1 #include <iostream>
2 #include <cstdio>
3 #include <queue>
4 using namespace std;
5
6 #define maxn 110 //最大頂點個數
7 #define INF 0xffffff //權值上限
8 int w[maxn][maxn]; //鄰接矩陣,存儲權值
9 int n; //頂點個數
10
11 struct node //頂點節點,保存id和到源頂點的估算距離,優先隊列需要的類型
12 {
13 int id, weight; //源頂點id和估算距離
14 friend bool operator<(node a, node b) //因要實現最小堆,按升序排列,因而需要重載運算符,重定義優先級,以小為先
15 {
16 return a.weight > b.weight;
17 }
18 };
19 priority_queue<node> q; //優先隊列,最小堆,實現Dijkstra的重要數據結構,用stl實現
20 int parent[maxn]; //每個頂點的父親節點,可以用於還原最短路徑樹
21 bool visited[maxn]; //用於判斷頂點是否已經在最短路徑樹中,或者說是否已找到最短路徑
22 node d[maxn]; //源點到每個頂點估算距離,最後結果為源點到所有頂點的最短路。
23 void Dijkstra(int s) //Dijkstra算法,傳入源頂點
24 {
25 for(int i = 1; i <= n; i++) //初始化
26 {
27 d[i].id = i;
28 d[i].weight = INF; //估算距離置INF
29 parent[i] = -1; //每個頂點都無父親節點
30 visited[i] = false;
31 }
32 d[s].weight = 0; //源點到源點最短路權值為0
33 q.push(d[s]); //壓入隊列中
34 while(!q.empty()) //算法的核心,隊列空說明完成了操作
35 {
36 node cd = q.top(); //取最小估算距離頂點
37 q.pop();
38 int u = cd.id;
39 if(visited[u])
40 continue;
41 visited[u] = true;
42 //松弛操作
43 for(int v = 1; v <= n; v++) //找所有與他相鄰的頂點,進行松弛操作,更新估算距離,壓入隊列。
44 {
45 if(v != u && !visited[v] && d[v].weight > d[u].weight+w[u][v])
46 {
47 d[v].weight = d[u].weight+w[u][v];
48 parent[v] = u;
49 q.push(d[v]);
50 }
51 }
52 }
53 }
54 int main()
55 {
56 int m, a, b, c, st, ed;
57 printf("請輸入頂點數和邊數:\n");
58 scanf("%d%d", &n, &m);
59 printf("請輸入邊以及權值(a, b, c)\n");
60 for(int i = 1; i <= n; i++) //鄰接矩陣存儲前需要初始化
61 for(int j = i; j <= n; j++)
62 w[i][j] = w[j][i] = INF;
63 while(m--)
64 {
65 scanf("%d%d%d", &a, &b, &c);
66 if(w[a][b] > c)
67 w[a][b]= w[b][a] = c;
68 }
69 printf("請輸入起點和終點:\n");
70 scanf("%d%d", &st, &ed);
71 Dijkstra(st);
72 if(d[ed].weight != INF)
73 printf("最短路徑權值為:%d\n", d[ed].weight);
74 else
75 printf("不存在從頂點%d到頂點%d的最短路徑。\n", st, ed);
76 return 0;
77 }
八、時間復雜度分析
不管用什麼方法,總共用時為O(V*T(EXTRACTION)+E*T(DECREASE))
(1)如果用數組來實現,總時間復雜度為O(V2)
(2)如果用二叉堆來實現,總時間復雜度為O(ElogV)
(3)如果使用斐波那契堆,總時間復雜度為O(E+VlogV)
上面的三種方法,越往下時間復雜度越好,但是實現難度越高,而且每次對最小優先隊列的更新是非常麻煩的,那麼,有沒有一種方法,可以不更新優先隊列也達到同樣的 效果呢?
答案是:有。
其實只需要簡單的操作就可以達到。首次只將根結點入隊列。第一次循環,取出隊列頂結點,將其退隊列,之後找到隊列頂的結點的所有相鄰頂點,若有更新,則更新它們 的key值後,再將它們壓入隊列。重復操作直至隊列空為止。因為對樹的更新是局部的,所以只需將相鄰頂點key值更新即可。push操作的復雜度為O(logV),而且省去了之前 將所有頂點入隊列的時間,因而總復雜度為O(ElogV)。
20分有點少啊。我以前寫過,晚上回去幫你找找。現在不在自己電腦旁邊。
這些是c++的代碼不知是否滿足你的要求。
1、鄰接表表示的圖中分別用DFS和BFS遍歷
#include <cstdio>
#include <cstring>
#include <queue>
using namespace std;
///////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
// Description: 圖的鄰接表的結點
struct Edge
{
int dest; // 目標結點下標
// int value; // 路徑長度
Edge *link; // 下一個結點
};
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////......余下全文>>