一、前瞻
在之前的單源最短路徑Dijkstra算法中，博主給出了最短路徑的一些基本概念和問題，並且給出了對權值不能為負的圖使用Dijkstra算法求解單源最短路徑問題的方法。
我們提到，Dijkstra算法的一個巨大前提是：不能有權值為負的邊。因為當權值可以為負時，可能在圖中會存在負權回路，最短路徑只要無限次地走這個負權回路，便可以無限制地減少它的最短路徑權值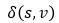
，這就變相地說明最短路徑不存在，Dijkstra算法無法終止。下圖說明從u到v的最短路徑是不存在的。
Bellman_Ford算法。有關最短路徑的相關問題以及Dijkstra算法的求解，可參看下列博客：
http://www.cnblogs.com/dzkang2011/p/sp_dijkstra.html
二、Bellman_Ford算法思想
如果圖G中存在負權回路，那麼某些最短路徑是不存在的。
Bellman_Ford算法的基本思想是：計算從源頂點s到其他所有頂點的最短路徑權值，若碰上負權回路，則報告存在負權回路並返回。
若圖中無負權回路，Bellman_Ford算法最多需要經過|V|-1次對所有邊的松弛操作，就可以得到結果（有關證明請google）。當結束|V|-1次操作之後，在外圍再做一次對所有邊的松弛操作的測試，若到某些頂點的最短路徑權值還能減小，說明|V|-1次松弛沒有得到最後結果，那麼必定存在負權回路，直接返回；若不再減小，說明已找到最短路。有關詳情可看偽代碼注釋。
偽代碼如下：
Bellman_Ford(G, w, s)
d[s]←0 //初始化，s到s最短路權值為0，其他為正無窮
for each v∈V-{s}
d[v]←∞
parent[v]← NIL //為生成最短路徑樹起作用
for i ← 1 to |V|-1 // 實驗證明最多只需|V|-1次外層循環，|V|-1次結束後，若圖G中無負權回路，那麼s到其他所有頂點的最短路徑求得
do for each edge (u, v)∈E //算法核心，松弛每一條邊，維持三角不等式成立
do if d[v] > d[u] + w(u, v)
then d[v] ← d[u]+w(u, v)
parent[v]←u
for each edge (u, v)∈E //進行完|V|-1次循環操作後，如果還能某條邊還能進行松弛，說明到某個點的最短路徑還未找到，那麼必定是存在負權回路，返回FALSE
do if d[v] > d[u] + w(u, v)
then return FALSE
return TRUE //若進行上面的松弛之後沒有返回，說明所有的d值都不會再改變了，那麼最短路徑權值完全找到，返回TRUE
三、簡單例子說明
下面給出一個簡單的例子來模擬Bellman_Ford算法的過程，因為在|V|-1次循環中，我們需要做的是試圖松弛每一條邊，為了方便起見，我們給每一條邊進行編號，然後按編號進行松弛，這樣的話計算機實現比較方便，而且對結果不會產生影響。
初始情況：
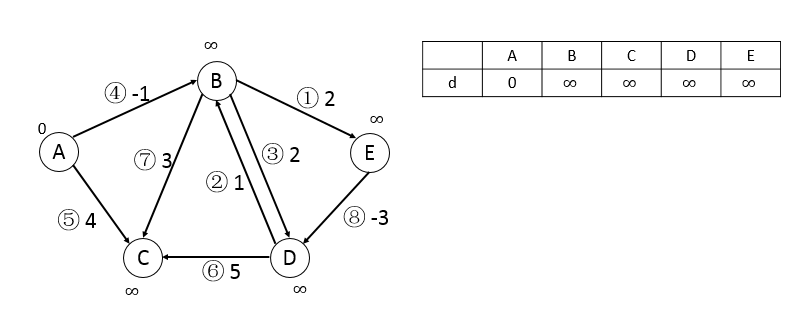
第一輪，按順序可松弛邊4和邊5，更新頂點B和C：
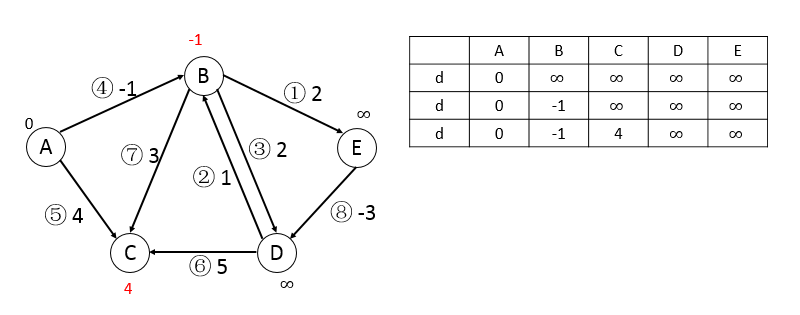
第二輪，按順序可松弛邊1、3、7、8，更新頂點E、D、C、D：
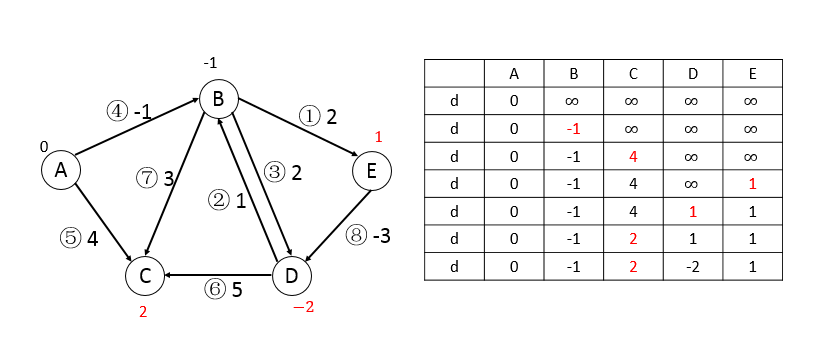
第三輪，進行一輪後發現無變化，跳出循環。
注：若存在負權回路，那麼|V|-1必定全部做完，因為每次都可以更新，減去這個負權回路的值。
四、代碼實現
下面給出Bellman_Ford算法的C/C++實現，其中可進行部分的優化。
我們發現，在進行|V|-1次循環操作時，每次的更新都與頂點的d的值有關，若所有d值不再改變了，那就不會影響到下一次的結果，那麼我們就可以提前跳出循環，避免下面不必要的操作。
實現：
1 #include <iostream>
2 #include <cstdio>
3 using namespace std;
4
5 #define INF 0xffff //權值上限
6 #define maxe 5000 //邊數上限
7 #define maxn 100 //頂點數上限
8 int n, m; //頂點數、邊數
9 int d[maxn]; //保存最短路徑權值的數組
10 int parent[maxn]; //每個頂點的前驅頂點，用以還原最短路徑樹
11 struct edge //表述邊的結構體，因為要對每一條邊松弛
12 {
13 int u, v, w; //u為邊起點，v為邊端點，w為邊權值，可以為負
14 }EG[maxe];
15
16 bool Bellman_Ford(int s) //計算從起點到所有頂點的
17 {
18 for(int i = 1; i <= n; i++) //初始化操作d[EG[j].v] > d[EG[j].u]+EG[j].w
19 {
20 d[i] = INF;
21 parent[i] = -1;
22 }
23 d[s] = 0;
24 bool flag; //標記，判斷d值是否更新，跳出外層循環的依據
25 for(int i = 1; i < n; i++) //外層循環最多做n-1次
26 {
27 flag = false; //初始為false,假設不需再更新
28 for(int j = 0; j < m; j++) //對m條邊進行松弛操作，若有更新，flag記為true
29 if(d[EG[j].v] > d[EG[j].u]+EG[j].w) //if d[v] > d[u] + w(u, v)，更新d[v]
30 {
31 d[EG[j].v] = d[EG[j].u]+EG[j].w;
32 parent[EG[j].v] = EG[j].u;
33 flag = true;
34 }
35 if(!flag) break; //若松弛完每條邊後，flag狀態不變，說明未發現更新，可直接跳出循環
36 }
37 for(int i = 0; i < m; i++) //做完上述松弛後，如果還能松弛，說明存在負權回路，返回false
38 if(d[EG[i].v] > d[EG[i].u]+EG[i].w)
39 return false;
40 return true; //不存在負權回路，返回true
41 }
42
43 int main()
44 {
45 int st;
46 printf("請輸入n和m:\n");
47 scanf("%d%d", &n, &m);
48 printf("請輸入m條邊(u, v, w)：\n");
49 for(int i = 0; i < m; i++)
50 scanf("%d%d%d", &EG[i].u, &EG[i].v, &EG[i].w);
51 printf("請輸入起點：");
52 scanf("%d", &st);
53 if(Bellman_Ford(st))
54 {
55 printf("不存在負權回路。\n");
56 printf("源頂點到各頂點的最短路徑權值為：\n");
57 for(int i = 1; i <= n; i++)
58 printf("%d ", d[i]);
59 printf("\n");
60 }
61 }
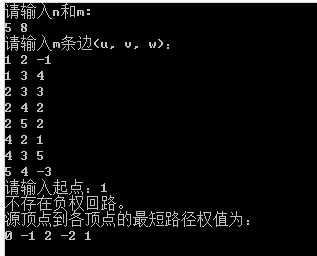
五、測試結果
就上面例子，我們進行測試，其中點都換成了數字形式：
六、時間復雜度分析
Bellman_Ford算法實現起來相比使用優先隊列的Dijkstra算法要簡單許多，但是時間復雜度不如Dijkstra算法，從代碼分析，我們可以看出它的復雜度為O(VE)，V表示頂點個數，E表示邊的條數。但是，至少現在我們可以對負權值情況進行求解。
（轉載請注明出處。）
比如：A上班離家裡很遠，他要選擇一條從家裡到公司的最佳路徑，使得費用最小。而公司的話，對於做公交車的那段路有補貼，且補貼的錢大於坐公交車的費用，此時，在計算最小費用的時候，這條邊的權值就應該定義為負值
記dijakstra算法為D算法
D算法為貪心算法,每一步的選擇為當前步的最優,復雜度為O(n*n) (又叫爬山法)
分支限界算法,每一步的擴散為當前耗散度的最優,復雜度為(沒算)
都是A算法的極端情況
(說錯了哈,下面我的文字中的的分支限界算法實際上是在說動態規劃法,我查了一下書,動態規劃法是對分支限界法的改進,分支限界法不屬於A算法(啟發式搜索算法),但是這時用動態規劃法和D算法比較也是有可比性的,而直接用分支限界算法和D算法比較也是可以的)
關鍵詞:耗散度 評估函數
即:對當前優先搜索方向的判斷標准為,有可能的最優解
而最優解可以用一個評估函數來做,即已經有的耗散度加上以後有可能的耗度
A算法就是把兩個耗散度加在一起,作為當前狀態的搜索搜索方向;
但是對以後的耗散度的評估是麻煩的,D算法就是把當前有的路的最短的作為,以後耗散度的評估.
分支限界算法就是只以以前的耗散度為評估函數
你給的兩個算法當然是A算法的特例
你還可以參考一下 A*算法 修正的A*算法,相信對你的編程水平有幫助
參考:
隊列式分支限界法的搜索解空間樹的方式類似於解空間樹的寬度優先搜索，不同的是隊列式分支限界法不搜索以不可行結點（已經被判定不能導致可行解或不能導致最優解的結點）為根的子樹。按照規則，這樣的結點不被列入活結點表。
優先隊列式分支限界法的搜索方式是根據活結點的優先級確定下一個擴展結點。結點的優先級常用一個與該結點有關的數值p來表示。最大優先隊列規定p值較大的結點點的優先級較高。在算法實現時通常用一個最大堆來實現最大優先隊列，體現最大效益優先的原則。類似地，最小優先隊列規定p值較小的結點的優先級較高。在算法實現時，常用一個最小堆來實現，體現最小優先的原則。采用優先隊列式分支定界算法解決具體問題時，應根據問題的特點選用最大優先或最小優先隊列，確定各個結點點的p值。
