程式師世界 >> 編程語言 >> C語言 >> C++ >> C++入門知識 >> 快排、歸並排序（分治）、堆排序

快排、歸並排序（分治）、堆排序

編輯：C++入門知識

一、快速排序

1）算法簡介

快速排序是由C. A. R. Hoare所發展的一種排序算法。其基本思想是基本思想是，通過一趟排序將待排記錄分隔成獨立的兩部分，其中一部分記錄的關鍵字均比另一部分的關鍵字小，則可分別對這兩部分記錄繼續進行排序，以達到整個序列有序。

2）算法描述

快速排序使用分治法來把一個串（list）分為兩個子串行（sub-lists）。
步驟為：
1、從數列中挑出一個元素，稱為 "基准"（pivot），
2、重新排序數列，所有元素比基准值小的擺放在基准前面，所有元素比基准值大的擺在基准的後面（相同的數可以到任一邊）。在這個分區退出之後，該基准就處於數列的中間位置。這個稱為分區（partition）操作。
3、遞歸地（recursive）把小於基准值元素的子數列和大於基准值元素的子數列排序。
最差時間復雜度：O(n^2)
最優時間復雜度：O(n log n)
平均時間復雜度：O(n log n)
最差空間復雜度：根據實現的方式不同而不同

3）算法代碼

快速排序有很多版本，但關鍵是劃分的思想。

void QuickSort(int L[], int l, int r)
{
	int i, j, pivot;

	if(l >= r)
		return;
	//std::swap(L[l], L[(l+r)/2]);//以中間的數作為基准數的
	//int p = l + rand() % (r - l + 1);	  //rand_partition()
	//std::swap(L[l], L[p]);
	i = l, j=r, pivot = L[l];
	while(i < j)
	{
		while(i < j && L[j] >= pivot)//從右向左找第一個比key小的數
			j--;
		if(i < j)
			L[i++] = L[j];

		while(i < j && L[i] <= pivot)//從左向右找第一個比key大的數
			i++;
		if(i < j)
			L[j--] = L[i];
	}
	L[i] = pivot;
	QuickSort(L, l, i-1);
	QuickSort(L, i+1, r);
}

void qsort1(int L[], int l, int r)
{
	if (l >= r)
		return;
	int i = l, j;
	for (j = l + 1; j <= r; j++)	  
		/* invariant: L[l+1..i] < L[l] && L[i+1..j-1] >= L[l]*/
		if (L[j] < L[l])	 //<
			std::swap(L[++i], L[j]);
	std::swap(L[l], L[i]);
	/* L[l..i-1] < L[i] <= L[i+1..r]*/
	qsort1(L, l, i - 1);
	qsort1(L, i + 1, r);
}

void qsort3(int L[], int l, int r)
{
	if (l >= r)
		return;
	int pivot = L[l];
	int i = l, j = r + 1;
	while(i <= j)
	{
		do 
		{
			i++;
		} while (i <= r && L[i] < pivot);
		do 
		{
			j--;
		} while (L[j] > pivot);
		if (i > j)
			break;
		std::swap(L[i], L[j]);
	}
	std::swap(L[l], L[j]);
	qsort3(L, l, j - 1);
	qsort3(L, j + 1, r);
}

void qsort4(int L[], int l, int r)
{
	if (l >= r)
		return;
	int pivot = L[l];
	int i = l - 1, j = r + 1;
	while(i <= j)
	{
		do 
		{
			i++;
		} while (/*i <= r &&*/ L[i] < pivot);
		do 
		{
			j--;
		} while (L[j] > pivot);
		if (i > j)
			break;
		std::swap(L[i], L[j]);
	}
	//print(L, l, r);putchar('\n');
	std::swap(L[l], L[j]);
	qsort3(L, l, j - 1);
	qsort3(L, j + 1, r);
}

4）利用快排劃分細思想求數組第k小的數，或者最小的前k個數

（1）第k小的數

//一次劃分後，主元左邊的數都小於主元，主元右邊的數都大於或者等於主元
int Rand_Partition(int A[], int l, int r)
{
    int i, j, pivot;
    
    int p = l + rand()% (r - l + 1);
    std::swap(A[l], A[p]);
    
    pivot = A[l], i = l, j = r;
    while(i < j)
    {
        while(i < j && A[j] >= pivot)  //從右向左找第一個小於pivot的數
            j--;
        if(i < j)
            A[i++] = A[j];
        while(i < j && A[i] < pivot)  //從左向右找第一個大於或等於pivot的數
            i++;
        if(i < j)
            A[j--] = A[i];
    }
    A[i] = pivot;
    
    return i;
}

int Rand_Select(int A[], int l, int r, int i) //ith big in A[l, ..., r]
{
    int pivotloc, k;

    if(l == r)
        return A[l];

    pivotloc = Rand_Partition(A, l, r);
    k = pivotloc - l + 1;

    if(i == k)
        return A[pivotloc];
    else if(i < k)
        return Rand_Select(A, l, pivotloc-1, i);
    else
        return Rand_Select(A, pivotloc+1, r, i-k);
}

（2）最小的前k個數可以建立含有k個元素的大頂堆求解。也可以利用劃分的思想,代碼如下：

void GetleastNumber(int input[], int n, int output[], int k)
{
	if (n <= 0 || k <= 0 || k > n)
		return;

	int l = 0, r = n - 1;
	int pivotloc = Partition(input, l, r);

	//l..|....|.....|...r
	//	 p < k-1 <= p

	while (pivotloc != k - 1)
	{
		if (pivotloc < k - 1)
		   pivotloc = Partition(input, pivotloc + 1, r);
		else
		   pivotloc = Partition(input, l, pivotloc - 1);
	}
	memcpy(output, input, k * sizeof(int));
}

二、歸並排序

1）算法簡介

歸並排序是建立在歸並操作上的一種有效的排序算法。該算法是采用分治法（Divide and Conquer）的一個非常典型的應用。歸並排序是一種穩定的排序方法。

將已有序的子序列合並，得到完全有序的序列；即先使每個子序列有序，再使子序列段間有序。若將兩個有序表合並成一個有序表，稱為2-路歸並。

2）算法描述

歸並排序具體算法描述如下(遞歸版本)：

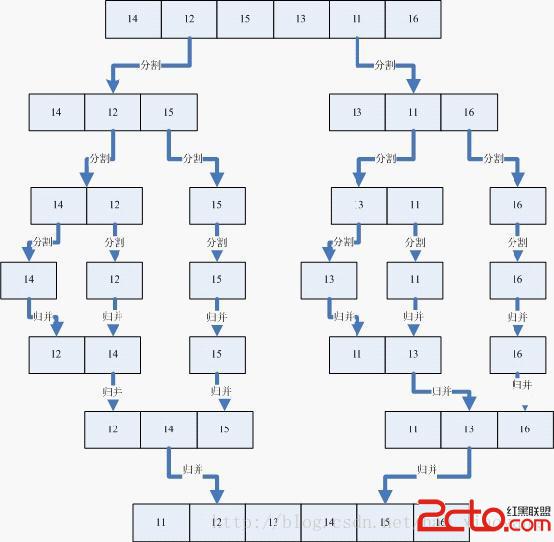
1、Divide: 把長度為n的輸入序列分成兩個長度為n/2的子序列。

2、Conquer: 對這兩個子序列分別采用歸並排序。

3、Combine: 將兩個排序好的子序列合並成一個最終的排序序列。

歸並排序的效率是比較高的，設數列長為N，將數列分開成小數列一共要logN步，每步都是一個合並有序數列的過程，時間復雜度可以記為O(N)，故一共為O(N*logN)。因為歸並排序每次都是在相鄰的數據中進行操作，所以歸並排序在O(N*logN)的幾種排序方法（快速排序，歸並排序，希爾排序，堆排序）也是效率比較高的。

3）算法代碼

歸排序代碼的寫法可以有集中，下面分別給出：（1）首先分配好一個臨時數組空間，避免歸並函數內頻繁申請內存

//將兩個有序的數組a[first,...,mid], a[mid+1,...,last]合並成一個有序的（借助temp數組）
void MergeTwoSortedArray(int a[], int first, int mid, int last, int temp[])
{
	int i = first, j = mid + 1;
	int k = 0;
	while ( i <= mid && j <= last)
		if (a[i] < a[j])
			temp[k++] = a[i++];
		else
			temp[k++] = a[j++];

	while (i <= mid)
		temp[k++]  = a[i++];
	while (j <= last)
		temp[k++] = a[j++];

	//for (i = 0; i < k; i++)
	//	a[first + i] = temp[i];
	memcpy(a + first, temp, sizeof(int) * (last - first + 1));
}
 
//遞歸地對a[first,...,last]區間的元素二分排序再合並
void MergeSortR(int a[], int first, int last, int temp[])
{
	if (first < last)
	{
		int mid = (first + last) / 2;	     //將a[first, last]平分為a[first,...,mid]和a[mid+1,...,last]
		MergeSortR(a, first, mid, temp);     //左邊有序:遞歸地將a[first,...,mid]歸並為有序的temp[first,...,mid]
		MergeSortR(a, mid + 1, last, temp);	 //右邊有序:遞歸地將a[mid+1,...,last]歸並為有序的temp[mid+1,...,last]
		MergeTwoSortedArray(a, first, mid, last, temp);	//合並後全部有序:將有序的temp[first,...,mid]和有序的temp[mid+1,...,last]歸並到a[first, last]
	}
}

void MergeSort(int a[], int n)
{
	int *temp = new int[n];	  //臨時數組
	if (temp == NULL) return;
	memset(temp, 0, sizeof(int)*n);
	MergeSortR(a, 0, n - 1, temp);
	delete []temp;
}

（2）如果每次在歸並函數內部分配臨時的數組空間，歸並函數的寫法也可以有幾種：

//先將左右有序序列拷貝到臨時數組後再直接歸並到原數組
void MergeTwoSortedArray1(int a[], int first, int mid, int last)
{
	int i, j;
	int n1 = mid - first + 1;
	int n2 = last - mid;
	int *L = new int[n1];	//臨時數組
	int *R = new int[n2];

	//for (i = 0; i < n1; i++)   //左邊有序序列
	//	L[i] = a[first + i];
	//for (j = 0; j < n2; j++)
	//	R[j] = a[mid + 1 + j];	//右邊有序序列

	for (i = first; i <= mid; i++)
		L[i - first] = a[i];
	for (j = mid + 1; j <= last; j++)
		R[j - mid - 1] = a[j];

	i = 0, j = 0;
	int k = first;
	while (i < n1 && j < n2)
	{
		if (L[i] < R[j])
			a[k++] = L[i++];
		else
			a[k++] = R[j++];
	}
	while (i < n1)
		a[k++] = L[i++];
	while (j < n2)
		a[k++] = R[j++];

	delete []L;
	delete []R;
}

//先將左右有序序列拷貝到臨時數組後再直接歸並到原數組(使用哨兵)
void MergeTwoSortedArray2(int a[], int first, int mid, int last)
{
	int i, j;
	int n1 = mid - first + 1;
	int n2 = last - mid;
	int *L = new int[n1 + 1];	//臨時數組,末尾為哨兵元素
	int *R = new int[n2 + 1];

	//for (i = 0; i < n1; i++)   //左邊有序序列
	//	L[i] = a[first + i];
	//for (j = 0; j < n2; j++)
	//	R[j] = a[mid + 1 + j];	//右邊有序序列
	//L[i] = INT_MAX, R[j] = INT_MAX;	 //末尾添加哨兵元素

	for (i = first; i <= mid; i++)
		L[i - first] = a[i];
	for (j = mid + 1; j <= last; j++)
		R[j - mid - 1] = a[j];
	L[i - first] = INT_MAX, R[j - mid - 1] = INT_MAX;

	i = 0, j = 0;
	for (int k = first; k <= last; k++)
	{
		if (L[i] < R[j])
			a[k] = L[i++];
		else
			a[k] = R[j++];
	}

	delete []L;
	delete []R;
}

void MergeSortR1(int a[], int first, int last)
{
	if (first < last)
	{
		int mid = (first + last) / 2;
		MergeSortR1(a, first, mid);
		MergeSortR1(a, mid + 1, last);
		MergeTwoSortedArray3(a, first, mid, last);
	}
}

void MergeSort1(int a[], int n)
{
	MergeSortR1(a, 0, n - 1);
}

4）求逆序對

利用歸並排序的思想可以實現求逆序數對

int Merge(int a[], int first, int mid, int last, int temp[])
{
	int inversion = 0;
	int i = first, j = mid + 1, k = 0;
	while (i <= mid && j <= last)
	{
		if (a[i] <= a[j])
		{
			temp[k++] = a[i++];
		}else	 //a[i] > a[j],而a[first,..,i,..,mid]遞增有序,因此a[i~mid]與a[j]構成逆序對,共mid-i+1個
		{
			temp[k++] = a[j++];
			inversion += mid - i + 1;
		}
	}
	while (i <= mid)
		temp[k++] = a[i++];
	while (j <= last)
		temp[k++] = a[j++];
	memcpy(a + first, temp, sizeof(int) * (last - first + 1));
	return inversion;
}

int MergeInversionR(int a[], int first, int last, int temp[])
{
	int inversion = 0;
	if (first < last)
	{
		int mid = (first + last) >> 1;
		inversion += MergeInversionR(a, first, mid, temp);	//找左半段的逆序對數目
		inversion += MergeInversionR(a, mid + 1, last, temp);//找右半段的逆序對數目
		inversion += Merge(a, first, mid, last, temp);		//在找完左右半段逆序對以後兩段數組有序，然後找兩段之間的逆序對。最小的逆序段只有一個元素。  
	}
	return inversion;
}

int MergeInversion(int a[], int n)
{
	int inversion = 0;
	int *temp = new int[n];
	memset(temp, 0, sizeof(int)*n);
	inversion = MergeInversionR(a, 0, n - 1, temp);
	delete []temp;
	return inversion;
}