766 - Sum of powers
題意:求
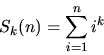
轉化成
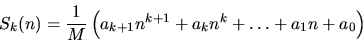
的各系數
思路:在wiki看了伯努利數的性質,
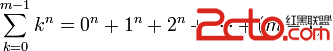
可以推成
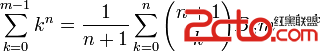
。
然後B為伯努利數,有公式
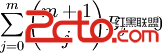
,
如此一來就可以去遞推求出每項伯努利數了,然後在根據n去通分,求出每一項的答案,中間過程用到了分數的運算。
代碼:
#include
#include
long long gcd(long long a, long long b) {
if (!b) return a;
return gcd(b, a % b);
}
long long lcm(long long a, long long b) {
a = a / gcd(a, b) * b;
if (a < 0) a = -a;
return a;
}
struct Fraction {
long long a, b;
Fraction() {a = 0; b = 1;}
Fraction(long long x) {
a = x; b = 1;
}
Fraction(long long x, long long y) {
a = x; b = y;
}
void deal() {
if (b < 0) {b = -b; a = -a;}
long long k = gcd(a, b);
if (k < 0) k = -k;
a /= k; b /= k;
}
Fraction operator+(Fraction p) {
Fraction ans;
ans.b = lcm(b, p.b);
ans.a = ans.b / b * a + ans.b / p.b * p.a;
ans.deal();
return ans;
}
Fraction operator-(Fraction p) {
Fraction ans;
ans.b = lcm(b, p.b);
ans.a = ans.b / b * a - ans.b / p.b * p.a;
ans.deal();
return ans;
}
Fraction operator*(Fraction p) {
Fraction ans;
ans.a = a * p.a;
ans.b = b * p.b;
ans.deal();
return ans;
}
Fraction operator/(Fraction p) {
Fraction ans;
ans.a = a * p.b;
ans.b = b * p.a;
ans.deal();
return ans;
}
void operator=(int x) {
a = x;
b = 1;
}
void print() {
printf("%lld/%lld\n", a, b);
}
};
const int N = 25;
Fraction B[N], C[N][N], a[N];
int n, t;
long long L;
void init() {
for (int i = 0; i < N; i++) {
C[i][0] = 1;
C[i][i] = 1;
for (int j = 1; j < i; j++) {
C[i][j] = C[i - 1][j - 1] + C[i - 1][j];
}
}
B[0] = 1;
for (int i = 1; i <= 20; i++) {
B[i] = 0;
for (int j = 0; j < i; j++) B[i] = B[i] - C[i + 1][j] * B[j];
B[i] = B[i] / C[i + 1][i];
}
}
int main() {
init();
scanf("%d", &t);
while (t--) {
L = 1;
scanf("%d", &n);
for (int i = 0; i <= n; i++) {
a[i] = C[n + 1][i] * B[i] * Fraction(1, n + 1);
L = lcm(L, a[i].b);
}
printf("%lld ", L);
a[1] = a[1] + 1;
for (int i = 0; i <= n; i++)
printf("%lld ", L / a[i].b * a[i].a);
printf("0\n");
if (t) printf("\n");
}
return 0;
}
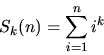 轉化成
轉化成 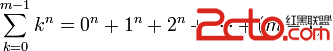 可以推成
可以推成 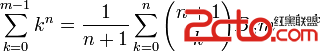 。
。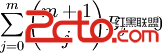 ,
,