[LeetCode]Linked List Cycle II解法學習

問題描述如下：

Given a linked list, return the node where the cycle begins. If there is no cycle, return null.

Follow up:

Can you solve it without using extra space?

　　從問題來看，如果可以充分利用額外空間的話，這個題目是不難的，然而題目提出了一個要求，能否在不使用任何額外空間的情況下解決這個問題。

　　通過反復思考，我覺得這題類似於追擊問題，可以用一個快速遍歷指針和一個慢速遍歷指針對這個鏈表進行遍歷，如果存在環，那麼這個快速指針肯定會在環中某一處追到這個慢指針。盡管有這樣的想法，但是在判斷出了是否有環之後，該如何進一步獲取環的起點呢？個人能力有限，之前沒有做過類似的題目，本著學習的目的，於是我查閱了資料，在LeetCode的討論區裡得到了解答：

　　設立一個慢指針slow，一個快指針fast，慢指針每次走一步，快指針每次走兩步。假設從head到環起點start的距離為x，環的長度為y（即從起點走回起點所需要走的步數）。

　　我們知道，當存在環的時候，fast和slow必然會在環中某一處相遇，假設相遇點距離start為m，於是slow和fast在m處相遇時，slow走了：x+ky+m，fast走了：x+ty+m。因為fast走的為slow的兩倍，於是：

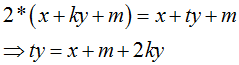
　　ty可以被y整除，所以x+m+2ky應當也能被y整除，即(x+m) mod y=0。於是，可以推斷，當二者在m出相遇時，再繞環走x步，便一定可以到達環的起點。

　　可得出代碼如下：

class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        if(!head) return NULL;
        ListNode* slow = head;
        ListNode* fast = head;
        do{
            if(!fast) return NULL;
            slow = slow->next;
            fast = fast->next;
            if(fast) fast = fast->next;
            else return NULL;
        }while( slow != fast );
        slow = head;
        while( slow != fast ){
            slow = slow->next;
            fast = fast->next;
        }
        return slow;
    }
};