LeetCode:Longest Valid Parentheses

Given a string containing just the characters '(' and ')', find the

length of the longest valid (well-formed) parentheses substring.For "(()", the

longest valid parentheses substring is "()", which has length = 2.

Another example is ")()())", where the longest valid parentheses substring

is "()()", which has length = 4.

解題思路:

這題可以用棧或者dp做，不過自己用棧寫的O(N)的解法沒有dp的快，所以說下dp的思路吧.

首先，看下狀態的定義:

dp[i]:表示選了第i個字符能組成的最長有效括號個數. 通過上面狀態的定義，很容易得出下面的狀態轉移方程: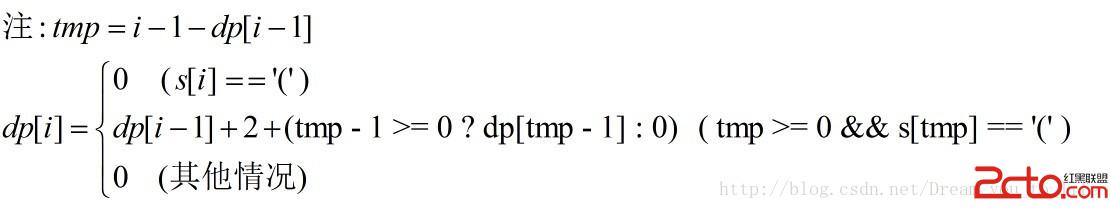


這裡解釋下第二個狀態方程的得來，當s[i]=")'時，tmp表示的就是與s[i]對應的那個字符，如果其滿足條件
(tmp>=0 && s[tmp]=='(')那麼就說明tmp到i這部分是有效括號匹配，而tmp之前的也有可能存在有效括號匹
配，所以需要將兩者相加，需要注意的是，邊界的地方.
解題代碼:

class Solution {
public:
    int longestValidParentheses(string s) 
    {
        int n = s.size(), dp[n];
        dp[0] = 0;
        for (int i = 1; i < n; ++i)
        {
            int tmp = i - 1 - dp[i - 1];
            if (s[i] == '(')
                dp[i] = 0;
            else if (tmp >= 0 && s[tmp] == '(')
                dp[i] = dp[i - 1] + 2 + (tmp - 1 >= 0 ? dp[tmp - 1] : 0);
            else
                dp[i] = 0;
        }
        return *max_element(dp, dp + n);
    }
};