給定一系列的點,和一個矩形。求矩形中包含的點的數量。
這個問題可以通過建立矩陣來進行求解。首先將一個空間分割成矩陣,將點放置在對應的格子中,再計算矩形覆蓋的格子,再判斷格子中的點是否包含在矩形中
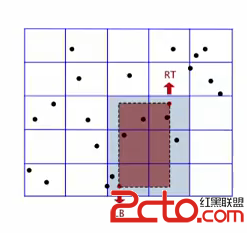
這種方法的問題是,可能這些點全都集中在一個格子中。這種情況下算法的效率比較低。
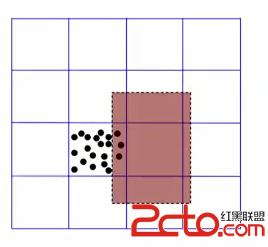
這種問題在地圖的應用中非常常見。
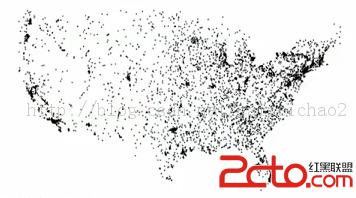
因此需要引入2D樹的概念,使得矩陣的分解會根據點的密度自動適應。
下圖展示了2D樹的樣子。
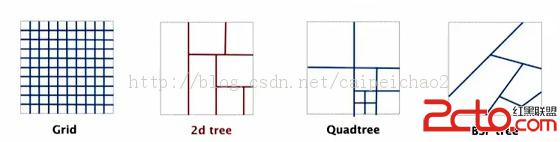
每次加入一個點時,將平面分成兩半。
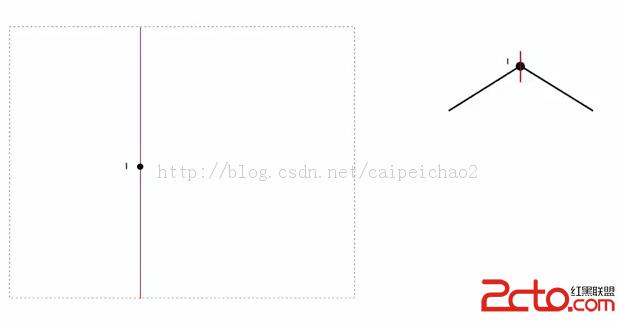
加入第二個點時,由於第二個點在第一個點的右側,因此在第一個點的右子節點創建一個新的節點。由於父節點是豎直的,所以子節點需要水平分割。
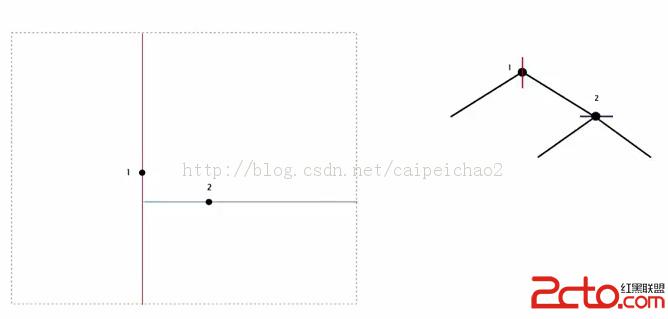
增加更多的點之後,就會形成如下的二叉樹。
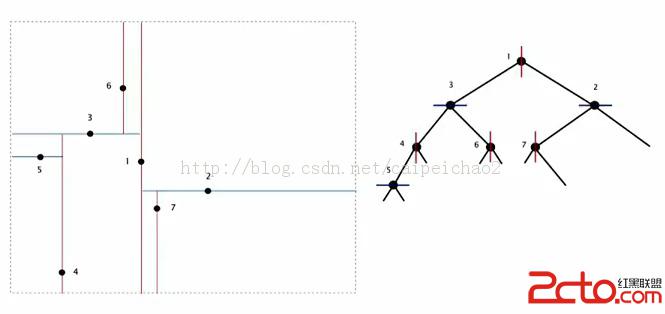
搜索矩形中包含的點。
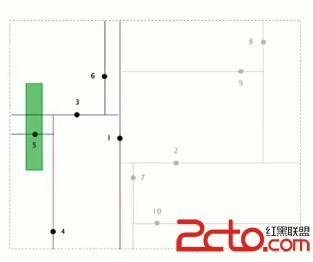
搜索的時候需要從根節點開始。從根節點知道,矩形在節點的左側,因此只需要搜索左側即可。到了點3,由於矩形覆蓋了兩邊的區域,因此需要搜索兩邊。一直迭代循環,直到節點搜索完畢為止。
這種算法的平均復雜度是logN,最壞復雜度是sqrtN。
給定一系列點,和一個待測點。求與待測點最近的點。
用2D樹的數據結構時,有時可以將搜索范圍縮小到一半。
Kd樹就是2D樹的推廣形式,處理二維以上的數據時非常高效。
N體模擬算法
關鍵思想就是對於單個質點來說,將距離較遠的那些點看成一個質點。
具體實現可以參考論文
http://www.cs.montana.edu/courses/spring2005/580/papers/0906008.pdf