快速排序和歸並排序一樣,也使用了分治思想。
最關鍵的步驟是分解,例如,對數組A[p..r]進行分解。劃分為2個子數組A[p..q - 1]和A[q + 1..r]。A[p..q - 1]中每一個元素都小於等於A[q],A[q + 1..r]中的每一個元素都大於等於A[q]。
偽碼:

![]()
1 PARTITION(A,p,r)
2 {
3 x = A[r];
4 i = p - 1;
5 for j = p to r -1
6 if A[j] <= x
7 i = i + 1
8 exchange A[i] with A[j]
9 exchange A[i + 1] with A[r]
10 return i + 1
11 }
View Code
分析:首先選擇數組的最後一個元素作為主元,i 設為第一個元素下標減1。A[p..r -1]中的元素依次與主元進行比較,如果比主元小,就和A[i + 1]交換,i加 1(第一個比主元小的交換到數組的第一個位置,第二個比主元小的交換到數組的第二個位置... ...)。循環結束後,子數組A[p..i]的元素都小於等於主元,子數組A[i + 1..r - 1]的元素都大於主元。最後把主元和A[i + 1]進行交換。最後數組A[p..r]就分解為2個子數組,子數組A[p..i]元素都小於等於A[i + 1],子數組A[i + 2..r]都大於A[i + 1]。
圖例:
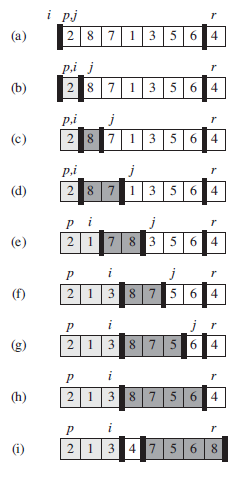
最後我們使用快速排序進行對數組的排序
偽碼:

![]()
1 QUICKSORT(A,p,r)
2 if p < r
3 q = PARTITION(A,p,r)
4 QUICKSORT(A,p,q - 1)
5 QUICKSORT(A,q + 1, r)
View Code
當p小於等於r時,數組中只有一個元素,顯然是排序的。否則,分解為2個子數組,遞歸調用快速排序。
如果每次劃分時,2個子數組分別包含了n - 1 和 0 個元素時,快速排序出現最壞情況,T(n) = O(n^2)。平均情況下T(n) = O(nlgn)
C++代碼

![]()
1 #define EXCHANGE(a,b) int temp = a;a = b;b = temp;
2
3 int partition(int A[],int p,int r)
4 {
5 int x = A[r];
6 int i = p - 1;
7
8 for(int j = p; j < r;++j)
9 {
10 if(A[j] < x)
11 {
12 ++i;
13 EXCHANGE(A[i],A[j])
14 }
15 }
16
17 EXCHANGE(A[i + 1],A[r]);
18
19 return i + 1;
20 }
21
22 //快速排序,平均時間復雜度T(n) = O(nlgn)
23 void Quick_sort(int A[],int p,int r)
24 {
25 if(p < r)
26 {
27 int q = partition(A,p,r);
28 Quick_sort(A,p,q - 1);
29 Quick_sort(A,q + 1,r);
30 }
31 }
View Code



