歸並排序完全遵循分治模式,主要操作分為三步:
1.分解:分解待排序的n個元素序列為2個n/2個元素的子序列。
2.解決:使用歸並排序遞歸的排序兩個子序列。
3.合並:合並兩個已排序的子序列。
最重要的步驟就是合並2個已經排序的序列。例如:A和B都是從小到大排序的序列。依次對比A的第一個元素和B的第一個元素,把其中較小的元素出序列,插入到C中,直到兩個序列中的元素都為空。最後,C序列就是一個包含A序列和B序列且從小到排序的序列。
偽碼:

![]()
1 Merge(A,p,q,r)
2 n1 = q - p + 1
3 n2 = r - q
4 let L[1..n1 + 1] and R[1.. n2 + 1] be new arrays
5 for i = 1 to n1
6 L[i] = A[p + i - 1]
7 for j = 1 to n2
8 R[i] = A[q + j]
9 L[n1 + 1] = ∞
10 R[n2 + 1] = ∞
11 i = 1
12 j = 1
13 for k = p to r
14 if L[i] <= R[j]
15 A[k] = L[i]
16 i = i + 1
17 else
18 A[k] = R[i]
19 j = j + 1
View Code
上述偽碼中,其中A為待排序的數組,且A[p..q ]和A[q + 1..r]都是排序好的。9,10行中,在L,R最後插入一個值,作為哨兵值,每當出現哨兵值時,它不可能為較小的值,這樣可以簡化代碼,避免檢查L或R為空。
圖例:
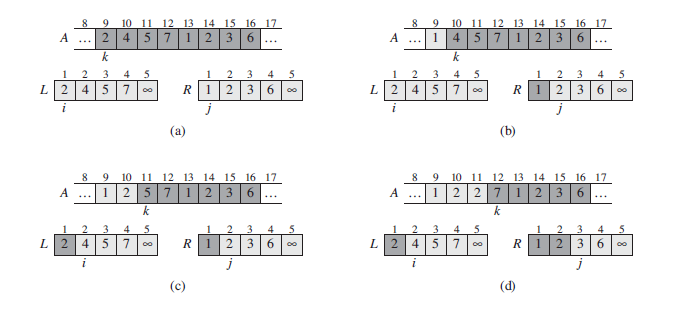
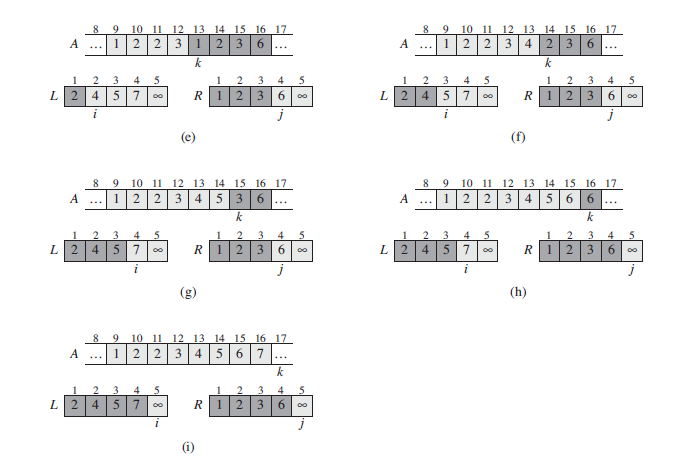
最後我們使用Merge_sort 排序數組A[p...r]中的元素。若p >= r,時,數組中最多只有一個元素,所以是排序好的,程序結束;否則,分解數組A[p...r]為兩個子數組A[p...q]和A[q + 1...r],然後合並2個子數組。
偽碼:

![]()
1 Merge_sort(A,p,r)
2 if p < r
3 q = ⌊(p + r) / 2⌋
4 Merge_sort(A,p,q)
5 Merge_sort(A,q + 1,r)
6 Merge(A,p,q,r)
View Code
圖例:
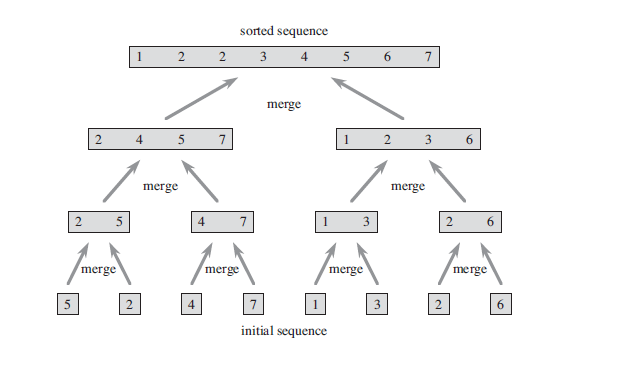
歸並排序的時間復雜度:T(n) = O(nlgn)
C++代碼:

![]()
1 void Merge(int a[],int p,int q,int r)
2 {
3 int n1 = q - p + 1;
4 int n2 = r - q;
5
6 int *L = new int[n1],*R = new int [n2];
7 for(int i = 0;i < n1;i++)
8 {
9 L[i] = a[p + i];
10 }
11 for(int i = 0;i < n2;i++)
12 {
13 R[i] = a[q + i + 1];
14 }
15
16 for(int k = p,iL = 0,iR = 0; k <= r;k++)
17 {
18 if(iL != n1 && iR == n2)
19 a[k] = *L++;
20 if(iR != n2 && iL == n1)
21 a[k] = *R++;
22
23 if(iL != n1 && iR != n2)
24 {
25 if(*L < *R)
26 {
27 a[k] = *L;
28 L++;
29 iL++;
30 }
31 else
32 {
33 a[k] = *R;
34 R++;
35 iR++;
36 }
37 }
38 }
39 delete[] (L - n1);
40 delete[] (R - n2);
41 }
42
43 //合並排序,T(n) = O(nlgn)
44 void Merge_sort(int a[],int p,int r)
45 {
46 if(p < r)
47 {
48 int q = (p + r) / 2;
49 Merge_sort(a,p,q);
50 Merge_sort(a,q + 1,r);
51 Merge(a,p,q,r);
52 }
53 }
View Code





