SICP 習題 （1.37）解題總結

SICP 習題 1.37是一條很長的題目，主要講的是無窮連分式。無窮連分式對我來說又是一個陌生的概念，於是又去百度了一番，發現無窮連分式也是一個很有意思的話題，涉及到無理數的表達。不過我建議大家還是暫時不要深入思考它的數學含義，一旦開始思考可能你又會跳進數學的深淵中不可自拔。

無窮連分式的形式如下：

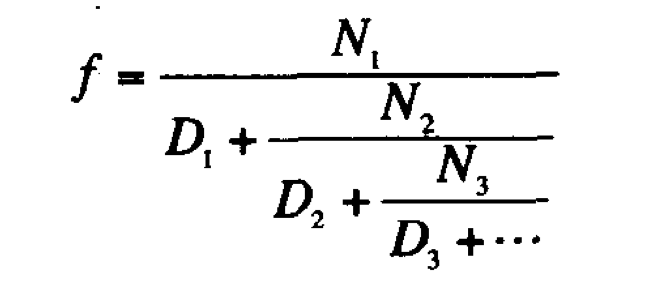
就像書中說到的，作為無窮連分式的一個特殊例子，如果N和D都為1的話，f= 1/ φ， 這點可以結合我們之前對黃金分割率的計算證明，這裡就不多說了，而且，如果你不能從數學上理解它也無所謂，不影響我們做題目，我們越來越強大了，強大到可以忽略題干中得數學定義直接完成習題。

題目進一步討論無窮連分式的計算，因為無窮連分式是無窮的，所以我們無法直接計算它的結果。為了計算一個無窮連分式的大概結果，簡單的辦法就是計算前面K個項，就像下面這樣：

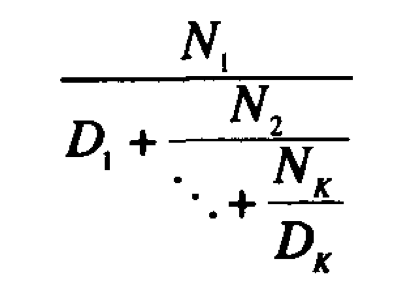
這樣我們就可以通過K 次計算完成某個無窮連分式的計算，當然，計算的結果是一個約數，不是准確數字。

題目要求我們完成一個名為cont-frac的過程，這個過程接受3個參數，分別是n, d 和k，其中n表示無窮連分式的N部分，d表示無窮連分式的D部分，k代表取幾個項進行計算。

如果我們仔細看無窮連分式的定義，就會發現這是一個很典型的遞歸定義。對於我們定義的cont-frac的過程，基本上它要做的事情就是：(cont-frac n) = N(n) / (D(n) + contact-frac(n+1))

除了上面的遞歸調用以外，cont-frac中還要完成的就是對k的比較，確定什麼時候結束遞歸調用，開始返回。

我定義的遞歸計算過程如下：

(define (cont-frac n d k)
  (define (cont-frac-inner n d cur-k)
    (if (< cur-k k)
	(/ (n cur-k) (+ (d cur-k) (cont-frac-inner n d (+ cur-k 1))))
	(d cur-k)))
  (cont-frac-inner n d 1))

(define (cont-frac-iter n d k)
  (define (cont-frac-iter-inner n d cur-k cur-value)
    (if (= cur-k k)
	(cont-frac-iter-inner n d (- cur-k 1) (d cur-k))
	(if (> cur-k 1)
	    (cont-frac-iter-inner n d (- cur-k 1) (+ (d cur-k) (/ (n cur-k) cur-value)))
	     (/ (n cur-k) cur-value))))

  (cont-frac-iter-inner n d k 0))

接著，題目還要求我們用這個cont-frac來計算黃金分割率，這個比較簡單，直接給n和d傳遞一個返回1的lambda過程就好了，我的測試方法如下:

(define (Phi-test k)
  (cont-frac (lambda (i) 1.0)
	     (lambda (i) 1.0)
	     k))

(define (Phi-test-iter k)
  (cont-frac-iter (lambda (i) 1.0)
	     (lambda (i) 1.0)
	     k))

最後，題目中還要求我們確定k取值多少的時候可以計算出有4位精度的黃金分割率，這就非常簡單了，多測試幾個cont-frac的調用就好了。