hdu3853 loops cf148D

先說一下cf148D的題意：有一條龍與一位王妃進行比賽。一個袋子裡裝有m只白老鼠b只黑老鼠，王妃與龍輪流從中摸一只老鼠，先摸到白老鼠的是贏家（王妃是先手），但是，龍摸老鼠的時候會驚嚇到其余的老鼠，會有一只老鼠從中自己跳出來（跳出來的老鼠如果是白色，不算任何人贏）。如果袋子裡沒有老鼠時還沒有決出勝負算龍勝。

dp[i][j]表示王妃的勝率。

很明顯dp[i][0](i > 0) = 1（只有白老鼠，王妃肯定贏）

dp[0][j] = 0（只有黑老鼠根據題意龍贏）

dp[i][j]可以轉移到4個地方

1.王妃摸到白老鼠（贏）概率 1.0 * i / (i + j)

2.王妃摸到白老鼠，龍摸到黑老鼠（輸）概率1.0 * j / (i + j) * 1.0 * i / (i + j - 1)

3.王妃摸到黑老鼠，龍摸到黑老鼠，跳出來一只白老鼠（可能贏）概率1.0 * j / (i + j) * 1.0 * (j - 1) / (i + j - 1) * 1.0 * i / (i + j - 2)

4.王妃摸到黑老鼠，龍摸到黑老鼠，跳出來一只黑老鼠（可能贏）概率1.0 * j / (i + j) * 1.0 * (j - 1) / (i + j - 1) * 1.0 * (j - 2) / (i + j - 2)

所以王妃的勝率 = 第一種情況 + 第三種情況 * dp[i - 1][j - 2] + 第四種情況 * dp[i][j - 3]; （dp[i][j]可以轉移到dp[i - 1][j - 2],dp[i][j - 3]，而dp[i - 1][j - 2],dp[i][j - 3]又表示在這種情況下的勝率，所以要加上）

        for (int i = 1; i <= n; i++) dp[i][0] = 1.0;
        for (int j = 0; j <= n; j++) dp[0][j] = 0;
        for (int i = 1; i <= n; i++)
        {
            for (int j = 1; j <= m; j++)
            {
                dp[i][j] = 1.0 * i / (i + j);

                if (j >= 2)
                {
                    dp[i][j] += 1.0 * j / (i + j) * 1.0 * (j - 1.0) / (i + j - 1.0) * 1.0 * i / (i + j - 2.0) * dp[i - 1][j - 2];
                }
                if (j >= 3)
                {
                    dp[i][j] += 1.0 * j / (i + j) * 1.0 * (j - 1.0) / (i + j - 1.0) * 1.0 * (j - 2.0) / (i + j - 2.0) * dp[i][j - 3];
                }
            }
        }

那麼E1 = E1 * p1 + E2 * p2 + E3 * p3 + 2 (每次操作消耗2點法力)

為什麼上面的等式成立，假如現在知道了E1， E2， E3的期望，而E1轉移到這三個地方的概率也知道p1， p2， p3,那麼根據期望的定義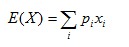，加上本次操作2點法力值，就是上面的等式，可以將後面的E1， E2， E3看作隨機變量X1, X2, X3。

等式化解後可以得到E1 = (E2 * p2 + E3 * p3) / (1 - p1) (1 - p1 != 0);

        for (int i = n; i >= 1; i--)
        {
            for (int j = m; j >= 1; j--)
            {
                if (i == n && j == m) continue;
                if (1.0 - temp[i][j][0] < eps) continue;
                dp[i][j] = (dp[i][j + 1] * temp[i][j][1] + dp[i + 1][j] * temp[i][j][2] + 2.0) / (1.0 - temp[i][j][0]);
            }
        }

        for (int i = n; i >= 0; i--)
        {
            if (i == n) continue;
            int p = i;

            while (mt[p]) p = mt[p];
            double temp = 0;

            if (p != i) dp[i] = dp[p];
            else
            {
                for (int j = 1; j <= 6; j++)
                {
                    if (p + j <= n)
                    {
                        temp += 1.0 / 6.0 * dp[p + j];
                    }
                }

                dp[i] = temp + 1.0;
            }
        }