題目如下：
A Strange Tree (S-tree) over the variable set 
is a binary tree representing a Boolean function
.Each path of the S-tree begins at the
root node and consists of n+1 nodes. Each of the S-tree's nodes has a
depth, which is the amount of nodes between itself and the root (so the root has depth 0). The nodes with depth less than
n are called non-terminal nodes. All non-terminal nodes have two children: the
right child and the left child. Each non-terminal node is marked with some variable
xi from the variable set Xn. All non-terminal nodes with the same depth are marked with the same variable, and non-terminal nodes with different depth are marked with different variables. So, there is
a unique variable xi1 corresponding to the root, a unique variable
xi2 corresponding to the nodes with depth 1, andso on. The sequence of the variables
is called the
variable ordering. The nodes having depth n are called terminal nodes. They have no children and are marked with either 0 or 1. Note that the variable ordering and the distribution of 0's and 1's on terminal nodes are sufficient to
completely describe an S-tree.
As stated earlier, each S-tree represents a Boolean function f. If you have an S-tree and values for the variables
,then it is quite simple to find out what
is: start with the root. Now repeat the following: if the node you are at is labelled with a variablexi,
then depending on whether the value of the variable is 1 or 0, you go its right or left child, respectively. Once you reach a terminal node, its label gives the value of the function.
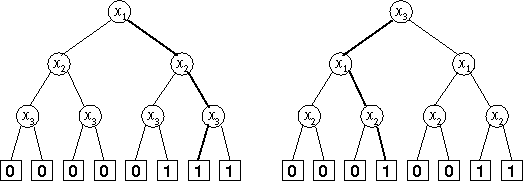
Figure 1: S-trees fZ喎?http://www.Bkjia.com/kf/ware/vc/" target="_blank" class="keylink">vciB0aGUgZnVuY3Rpb24gPGltZyBzcmM9"http://www.2cto.com/uploadfile/Collfiles/20140529/20140529092656200.gif" alt="$x_1 \wedge (x_2 \vee x_3)$" align="MIDDLE" border="0" height="34" width="109">
On the picture, two S-trees representing the same Boolean function, 
,are shown. For the left
tree, the variable ordering is x1, x2,
x3, and for the right tree it isx3, x1,
x2.
The values of the variables ,are given as a
Variable Values Assignment (VVA)
.For instance, (x1 = 1,
x2 = 1 x3 = 0) would be a valid VVA for
n = 3, resulting for the sample function above in the value 
.The corresponding paths are shown
bold in the picture.
Your task is to write a program which takes an S-tree and some VVAs and computesas described above.
,the depth of the S-tree. This is followed by a line describing the variable ordering of the S-tree. The format
of that line is xi1 xi2 ...xin. (There will be exactly
n different space-separated strings).So, for n = 3 and the variable ordering
x3, x1, x2, this line would look as follows:
x3 x1 x2
In the next line the distribution of 0's and 1's over the terminal nodes is given. There will be exactly 2n characters (each of which can be 0 or 1), followed by the new-line character.The characters are given in the order in which they appear in the S-tree, the first character corresponds to the leftmost terminal node of the S-tree, the last one to its rightmost terminal node.
The next line contains a single integer m, the number of VVAs, followed by m lines describing them. Each of the m lines contains exactly n characters (each of which can be 0 or 1), followed by a new-line character. Regardless of the variable ordering of the S-tree, the first character always describes the value of x1, the second character describes the value of x2, and so on. So, the line
110
corresponds to the VVA (x1 = 1, x2 = 1, x3 = 0).
The input is terminated by a test case starting with n = 0. This test case should not be processed.
for each of the given
m VVAs, where f is thefunction defined by the S-tree.
Output a blank line after each test case.
3 x1 x2 x3 00000111 4 000 010 111 110 3 x3 x1 x2 00010011 4 000 010 111 110 0
S-Tree #1: 0011 S-Tree #2: 0011
只要把題意搞清楚了這道題還是很簡單的，按照正常思路先建樹再遍歷，直接模擬即可。遍歷的時候遍歷兩次，第一次賦值，第二次得出結果，輸入的時候我是把X忽略，根據X的下標確定每個節點的位置，然後在遍歷賦值的時候就可以根據這個下標給節點賦值。把建樹放在循環中使每次的數據互不干擾。
AC的代碼如下：
