程式師世界 >> 編程語言 >> C語言 >> C++ >> C++入門知識 >> 概率論快速學習03：概率公理補充

概率論快速學習03：概率公理補充

編輯：C++入門知識

原創地址: http://www.cnblogs.com/Alandre/ (泥沙磚瓦漿木匠),需要轉載的,保留下! Thanks

　　“應注意到一個析取命題的對立命題是由該析取命題各部分的對立內容構成的一個合取命題” ——奧卡姆的威廉著，《邏輯學論文》

Written In The Font

　　I like maths when i was young,but I need to record them. So I am writing with some demos of Python

Content

　　If two events, A and B are independent then the joint probability is

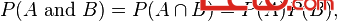
　　 $P(A \mbox{ and }B) = P(A \cap B) = P(A) P(B),\,$

For example, if two coins are flipped the chance of both being heads is

$\tfrac{1}{2}\times\tfrac{1}{2} = \tfrac{1}{4}.$

In Python

A = set([1,2,3,4,5])
B = set([2,4,3,5,6])
C = set([4,6,7,4,2,1])

print(A & B & C)

Output:

{2, 4}

# & find the objects the same in Set

　　 If either event A or event B or both events occur on a single performance of an experiment this is called the union of the events A and B denoted as:

　　 $P(A \cup B)$ .

　　If two events are mutually exclusive then the probability of either occurring is

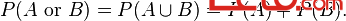
　　 $P(A\mbox{ or }B) = P(A \cup B)= P(A) + P(B).$

For example, the chance of rolling a 1 or 2 on a six-sided die is

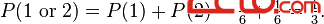
$P(1\mbox{ or }2) = P(1) + P(2) = \tfrac{1}{6} + \tfrac{1}{6} = \tfrac{1}{3}.$

In Python

A = set([1,2,3,4,5])
B = set([2,4,3,5,6])
C = set([4,6,7,4,2,1])

print(A | B | C)

Output:

{1, 2, 3, 4, 5, 6, 7}

# | find all the objects the set has

　　If the events are not mutually exclusive then

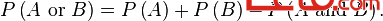
　　 $P\left(A \hbox{ or } B\right)=P\left(A\right)+P\left(B\right)-P\left(A \mbox{ and } B\right).$

Proved

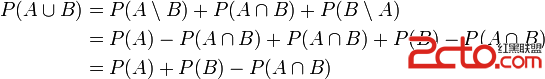
　　 $\begin{align}P(A\cup B) & =P(A\setminus B)+P(A\cap B)+P(B\setminus A)\\& =P(A)-P(A\cap B)+P(A\cap B)+P(B)-P(A\cap B)\\& =P(A)+P(B)-P(A\cap B)\end{align}$

For example:

　　Let’s use Python to show u an example about devil's bones (骰子,不是魔鬼的骨頭哈)

A = set([1,2,3,4,5,6])  # the all results of devil's bones
B = set([2,4,3])        # the A event results 
C = set([4,6])          # the B event results 

P_B =  1/2
P_C =  1/3

D = B | C
print(D)

P_D = 2/3

print(P_D == (P_B+P_C - 1/6))

Output:

{2, 3, 4, 6}
True

Let me show u some others :

$P(A)\in[0,1]\,$
$P(A^c)=1-P(A)\,$
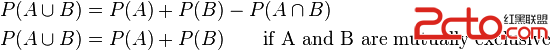
$\begin{align}P(A\cup B) & = P(A)+P(B)-P(A\cap B) \\P(A\cup B) & = P(A)+P(B) \qquad\mbox{if A and B are mutually exclusive} \\\end{align}$
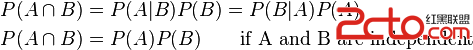
$\begin{align}P(A\cap B) & = P(A$
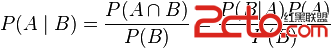
$P(A \mid B) = \frac{P(A \cap B)}{P(B)} = \frac{P(B$

If u r tired , please have a tea , or look far to make u feel better.If u r ok, Go on!

　　Conditional probability is the probability of some event A, given the occurrence of some other event B. Conditional probability is written:

　　 $P(A \mid B)$ ,

　　Some authors, such as De Finetti, prefer to introduce conditional probability as an axiom of probability:

$P(A \cap B) = P(A$ ^①

Given two events A and B from the sigma-field of a probability space with P(B) > 0, the conditional probability of A given Bis defined as the quotient of the probability of the joint of events A and B, and the probability of B:　　

　　 P(A ^②