當年實現自己的共享內存模板的時候,map和set的沒有實現,本來考慮用一個AVLTree作為底層實現的,為啥,因為我當時的數據結構知識裡面我和RBTree不熟,只搞過AVLTree,但當時我一直沒有看過刪除如何實現。結果Scottxu跳出來,參考STLport的實現,迅速用RBTree搞掂了。搞得這個代碼的頭文件也就一直放在那兒,7-8年後,整理這個代碼,看看Scottxu代碼的底子,覺得挺不錯的,覺得Copy改造一個AVLTree的實現應該很容易,就上手了。
AVL的插入無話可說,就是參考嚴蔚敏先生的《數據結構》上的手(仿佛回到十幾年前的大學時代),迅速搞掂,但到刪除,又啞火了。可以參考的代碼不多。特別把AVLTree刪除的代碼講明白的不多,有些明顯存在錯誤,有些是用高度Height計算的平衡因子,但大部分實現計算Height都是用遞歸,但這種消耗性能方法在正式環境基本不具備可操作性。於是看了一些帖子,自己摸索了一下實現,完善了基於每個節點自己保存平衡因子的結構算法(嚴蔚敏先生的《數據結構》樹中的插入也是基於平衡因子的),實現過程,發現小坑不少,總結出來。
(1)首先,仍然是找到這個要刪除的節點。
(2)然後要如果這個節點是葉子節點,直接刪除,如果不是葉子節點,需要將其交換成葉子節點。而交換方法是,選的其左子樹的最大節點(左子節點的最右兒子節點,),或者右子樹最小的節點(右子節點的最左兒子節點)。也就是選擇這個節點最相鄰的節點,和這個其交換。如果這個交換的位置還不是葉子節點,就繼續前面的方法找個節點交換。
當這個節點成為葉子節點,就刪除之。
示例一:10為要刪除的節點。經過2次交換,將其調整為節點3的位置,成為葉子節點
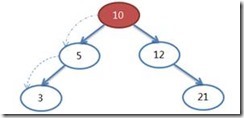
交換後的樹形變成:
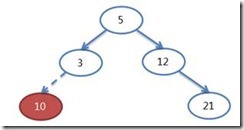
示例二:10為要刪除的節點。經過1次交換,將其調整為節點7的位置,成為葉子節點
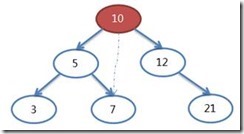
調整後的樹形變成:
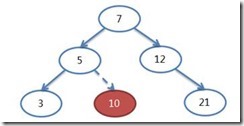
(3)刪除後,就要調整其父節點的平衡因子了。插入過程的時候,調整到平衡因子不等於0的節點就可以了。而刪除過程恰恰相反,調整到一個平衡因子為0的時候(高度變化對平衡的影響只到此為止),就可以停止。發現一個節點存在不平衡,平衡因子是2或者-2,那麼就需要做旋轉調整。而旋轉調整後,可能要繼續向上調整(這個和插入不太一樣),也可能停止調整(後面重點說明這個問題)。
如果是傳統意義的的LL,LR,RR,RL旋轉4種旋轉,那麼樹的高度會減少,所以還是要繼續向上調整平衡因子。
但有意思的是,由於刪除的特點,你會發現可能出現的情況,不全是傳統LL,LR,RR,RL 4種旋轉。比如,下面這個示例。
節點內部的()內為平衡因子,12為要刪除的節點,刪除後,節點7的平衡因子是2,但其左子節點5的平衡因子是0,這和LL(左子樹平衡因子為1)和LR旋轉(左子樹要平衡因子是-1)的情況都有一定的區別。
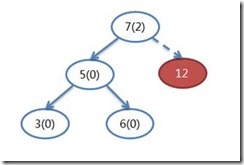
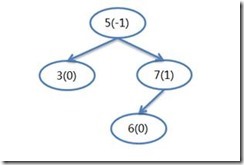
而這個樹形還是可以通過LL旋轉讓其平衡,但平衡之後,各個節點的平衡因子和插入後的平衡因子不一樣,根節點平衡因子沒有調整為0,而且發生這種情況下,樹的高度沒有發生變化,所以在刪除的情況下也不用繼續向上調整了。
同樣展示一下類似RR旋轉的一種情況:
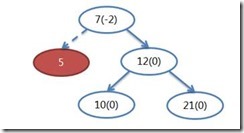
其調整後的樹形變成
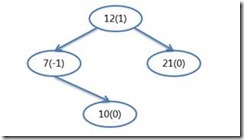
好了,基本情況如上所訴,參考代碼放在GIT,是基於模板的,類似STLPort。
算法這個東西,沒有看到明確明確說明前,碰還是謹慎一點,這次的測試過程畫了一堆的樹形圖。最後懷舊一下,當年在話單過濾的時候也寫過AVLTree(那時也沒有實現刪除),至今看看當年幼稚的代碼,而當年的大學時代的《數據結構》課程的代碼已經不知道在那張發霉的3吋軟盤上了,有些唏噓。好吧過兩天要去聽李宗盛的演唱會《既然青春留不住》了。
【本文作者是雁渡寒潭,本著自由的精神,你可以在無盈利的情況完整轉載此文檔,轉載時請附上BLOG鏈接:http://www.cnblogs.com/fullsail/,否則每字一元,每圖一百不講價。對Baidu文庫和360doc加價一倍】