循環求和中的代碼優化

在今天早上嵌入式課上的課前演示中，我提到了循環求和中的優化（其實那只是前一天我網上搜索做准備時無意碰到的）。演示中我舉的例程如下：

int sum = 0;
for (int i = 0; i < 100; i++)
{
    sum += array[i];
}
//*********我是分割線****************************
int sum1 = 0, sum2 = 0;
for (int i = 0; i < 100; i += 2)
{
    sum1 += array[i];
    sum2 += array[i + 1];
}
 
int sum = sum1 + sum2;

當時在網上看到的結論是，第二種方法更優，原因有二：一是循環體中兩個不相關的運算可以得到並行處理，減少運行時間；二是循環次數（從匯編的層次上講就是條件跳轉），其次數減少，因為條件跳轉只有到最後一刻才知道代碼會跳往何處。

演示完後，被老師問到，第二種方法能得到多大的優化，你測試過這代碼嗎？

悻悻地回答，沒有。

於是回來之後我用更大的循環次數去測試驗證了一下，代碼一如下：

#include 
#include 
int main()
{
    DWORD start_time,end_time;
    int sum,i;

    start_time=GetTickCount();
    sum=0;
    for(i=0;i<1000000000;i++)
        sum+=i;
    end_time=GetTickCount();
    printf("%d\n",end_time-start_time);

    sum=0;
    int sum2=0,sum3=0;
    start_time=GetTickCount();
    for(int i=0;i<1000000000;i+=2)
        sum2+=i,sum3+=i+1;
    sum=sum2+sum3;
    end_time=GetTickCount();
    printf("%d\n",end_time-start_time);
}

運行結果：

5594
3328

由此可見，第二種方法確實能得到可觀的性能優化。那麼，現在剩下的問題是，到底是第一個原因起的作用大，還是第二個原因？

我把第二種方法的代碼修改了，代碼二如下：

    sum=0;
    start_time=GetTickCount();
    for(int i=0;i<1000000000;i+=2)
        sum+=i+i+1;
    end_time=GetTickCount();
    printf("%d\n",end_time-start_time);

運行結果：

5422
2953

經常多次測試表明，代碼二確實比代碼一裡的第二種方法明顯快上一點。因此，我個人感覺其中沒有用到並行處理優化。也就是說，在特定的情況下，通過減少條件跳轉次數，可以獲得可觀的性能優化。

下面我嘗試進行-O編譯優化。結果如下：

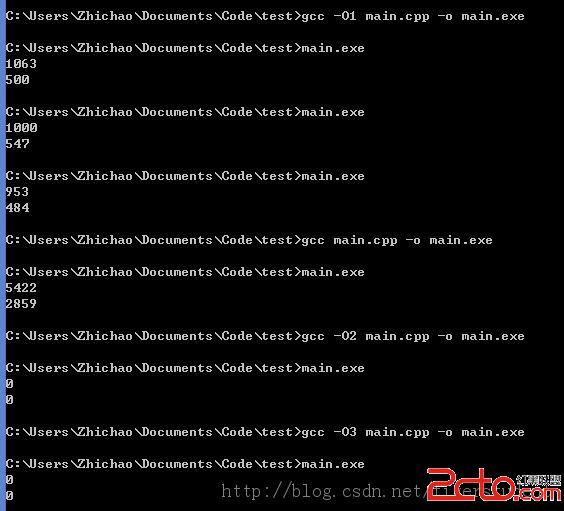
-O1優化居然能減少這麼多時間！不過可能是這段代碼邏輯太簡單了。另外不知道為什麼-O2優化後的運行結果不正常。。。有知道原因的童鞋請多多指教！