POJ 1958 Strange Towers of Hanoi (線性dp，記憶化搜索)

OJ題目：click here~~

題目分析：四柱漢諾塔。由於題目已經給出了求解方法，直接寫代碼即可。下面總結一下，四塔問題。

感謝這篇文章的作者，點這裡就到，總結的很好。直接貼過來~

四塔問題：設有A，B，C，D四個柱子(有時稱塔)，在A柱上有由小到大堆放的n個盤子。

今將A柱上的盤子移動到D柱上去。可以利用B，C柱作為工作棧用，移動的規則如下:
①每次只能移動一個盤子。
②在移動的過程中，小盤子只能放到大盤子的上面。
設計並實現一個求解四塔問題的動態規劃算法，並分析時間和空間復雜性。

算法思想:
用如下算法移動盤子(記為FourPegsHanoi):
1)、將A柱上n個盤子劃分為上下兩部分，下方部分共有k(1≤k≤n)個盤子，上方部分共有n - k個盤子。
2)、將A柱上面部分n–k個盤子使用FourPegsHanoi算法經過C、D柱移至B柱。
3)、將A柱剩余的k個盤子使用ThreePegsHanoi算法經過C柱移至D柱。
4)、將B柱上的n–k個盤子使用FourPegsHanoi算法經過A、C柱移至D柱。

ThreePegsHanoi算法如下(設三個柱子分別為A、B、C，A柱上共有k個盤子):
1)、將A柱上方k-1個盤子使用ThreePegsHanoi算法經過B柱移至C柱。
2)、將C柱上最後一個盤子直接移至C盤。
3)、將B柱上k-1個盤子使用ThreePegsHanoi算法經過A柱移至C柱。


算法步驟：
根據動態規劃的四個步驟，求解如下:
1)、最優子結構性質:
四柱漢諾塔問題的最優解是用最少的移動次數將A柱上的盤子全部移到D柱上。當盤子總數為i時，我們不妨設使用FourPegsHanoi的最少移動次數為f(i)。相應的ThreePegsHanoi 算法移動次數為g(k)，由於g(k)=2g(k-1)+1=pow（2，k） -1,當k確定時，g(k)也是不變的。
f(i)為最優解時，其子問題f(i-k)也必為最優解。如果f(i-k)不是最優解，那麼存在f’(i-k) < f(i-k)。用f’(i-k)替換f(i-k)將產生一個比f(i)更優的解。這與f(i)為最優解是矛盾的。所以本問題具有最優子結構性質。


2)、遞歸地定義問題的最優解:
根據上述FourPegsHanoi算法得到最少移動次數f(i):




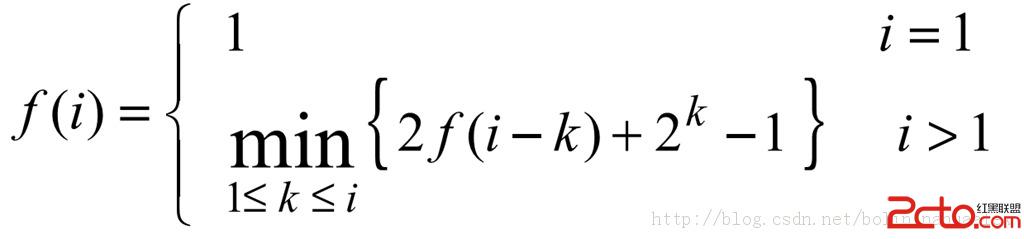
通過這個表達式我們可以知道，k取那個值時f(i)的值，也就是說，不用具體操作，就可以知道移動的最少次數，並且知道k的值，所以在算法實現時，求出k的值是非常重要的。下面的代碼就是用來求k的。

AC_CODE

//記憶化搜索
int dp[20];
int Move(int n){
    if(dp[n] != -1) return dp[n];
    int s = 1<<30;
    for(int i = 1;i <= n;i++){
        s =  min(s , 2 * Move(n - i) + (int)pow(2.0 , 1.0*i) - 1);
    }
    return dp[n] = s;
}

int main()
{   //freopen("in.txt","r",stdin);
    int i , j , k;
    for(i = 1;i <= 12;i++){
        memset(dp , -1 , sizeof(dp));
        dp[1] = 1;
        dp[0] = 0;
        cout << Move(i) << endl;
    }
    return 0;
}



//線性dp
int main()
{   //freopen("in.txt","r",stdin);
    int i , j , k;
    for(i = 0;i <= 13;i++) dp[i] = inf;
    dp[1] = 1;
    dp[0] = 0;
    for(i = 1;i <= 12;i++){
        for(j = 1;j <= i;j++)
            dp[i] = min(dp[i] , 2*dp[i - j] + (int)pow(2.0 , 1.0*j) - 1);
    }
    for(i = 1;i <= 12;i++){

        cout << dp[i] << endl;
    }
    return 0;
}