此博文主要講述了構造二叉樹的兩種方法:
1、通過先序和中序構造出二叉樹( 來自leetCode OJ上的 題目:Construct Binary Tree from Preorder and Inorder Traversal )
2、通過後序和中序構造出二叉樹( 來自leetCode OJ上的 題目:Construct Binary Tree from Inorder and Postorder Traversal)
這兩題的解法類似,下面我來詳細講下如何通過
二叉樹的先序序列和中序序列來構造出二叉樹,至於後序序列和中序序列就不著重講了哈!
題目:
Given preorder and inorder traversal of a tree, construct the binary tree.
Note:
You may assume that duplicates do not exist in the tree.
題目要求我們通過中序序列和先序序列來構造出這棵二叉樹,返回它的根節點。
那麼我們先模擬隨便畫出一棵二叉樹來,再把它的先序,中序,後序全部寫出來
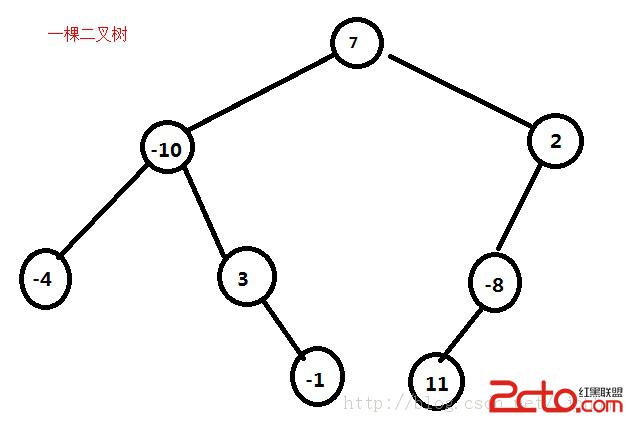
int[] preOrder = new int[]{7,-10,-4,3,-1,2,-8,11};
int[] pZ喎?http://www.Bkjia.com/kf/ware/vc/" target="_blank" class="keylink">vc3RPcmRlciA9IG5ldyBpbnRbXXstNCwtMSwzLC0xMCwxMSwtOCwyLDd9Ozxicj4KaW50W10gaW5PcmRlciA9IG5ldyBpbnRbXXstNCwtMTAsMywtMSw3LDExLC04LDJ9Ozwvc3Ryb25nPjxicj4KPC9wPgo8cD48YnI+CjwvcD4KPHA+PHN0cm9uZz694sziy7zCt6O6PC9zdHJvbmc+PC9wPgo8cD7I58nPo6zO0sPHtcO1vcHL0ru/w7b+subK97XEz8jQ8tDywdBwcmVPcmRlciA9IHs3LC0xMCwtNCwzLC0xLDIsLTgsMTF9O7rN1tDQ8tDywdBpbk9yZGVyCiA9IHstNCwtMTAsMywtMSw3LDExLC04LDJ9OzwvcD4KPHA+ztLDx8/r0qq5ub2os/bV4r/Dtv6y5sr3o6zEx8O0ztKyydPDtd256bXEt723qMC0yLe2qLP2w7+49r3hteO6zb3hteO85LXEudjPtTwvcD4KPHA+zai5/c/I0PLQ8sHQezcsLTEwLC00LDMsLTEsMiwtOCwxMX2jrM7Sw8e/ydLU1qq1wKOstdrSu7j2veG14ze/z7aoyse2/rLmyve1xLj5veG146Ostvi12rb+uPa94bXjLTEwo6zT0L/JxNzKx7j5veG147XE1/PX08r3tcS4+b3hteOjrNKy09C/ycTcysfT0tfTyve1xLj5veG146Oovt/M5bXDv7TW0NDy0PLB0NbQtcQg"7" 左邊是否還有其他的結點值,或者右邊是否還有其他的結點值),居然這個大問題可以被分解成小問題,我們選擇采用遞歸的方式來解決這個問題
1. 首先通過preOrder序列,得到根結點root!
2. 遞歸求出root的左子樹
3. 遞歸求出root的右子樹
4. 將左子樹的根結點賦值給root.left, 右子樹的根結點賦值給root.right
AC代碼(Construct Binary Tree from Preorder and Inorder Traversal ):
/**
* Definition for binary tree
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
public class Solution {
public TreeNode buildTree(int[] preorder, int[] inorder) {
if (preorder.length == 0 || inorder.length == 0)
return null;
int len = inorder.length;
return createTreeNode(preorder,inorder,0,len-1,0);
}
public TreeNode createTreeNode(int[] preorder, int[] inorder, int inLeft, int inRight, int preIndex){
//判斷是否為葉子結點
if (inLeft == inRight){
TreeNode node = new TreeNode(inorder[inLeft]);
node.left = null;
node.right = null;
return node;
}
//把preOrder中當前下標preIndex指向的val取出
int val = preorder[preIndex];
int findIndex = inLeft;
//找到val在inOrder中的位置(該子樹的根節點位置)
while (findIndex != inRight && val != inorder[findIndex]){
findIndex++;
}
TreeNode leftNode;
TreeNode rightNode;
//判斷是否有左右子樹,並創建出相應的左右子樹(如果val在inOrder中的位置下標等於inLeft,表明這個子樹是沒有左子樹的,而val在inOrder中的位置下標等於inRight,表明這個子樹沒有右子樹)
if (findIndex == inLeft){
leftNode = null;
}else{
leftNode = createTreeNode(preorder,inorder,inLeft,findIndex-1,++preIndex);
}
if (findIndex == inRight){
rightNode = null;
}else{
rightNode = createTreeNode(preorder,inorder,findIndex+1,inRight,++preIndex);
}
//把左右子樹賦值給root結點
TreeNode root = new TreeNode(val);
root.left = leftNode;
root.right = rightNode;
return root;
}
}AC代碼(Construct
Binary Tree from Inorder and Postorder Traversal)
/**
* Definition for binary tree
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
public class Solution {
private int postIndex;
public TreeNode buildTree(int[] inorder,int[] postorder) {
if (postorder.length == 0 || inorder.length == 0)
return null;
int len = inorder.length;
postIndex = postorder.length - 1;
return createTreeNode(postorder,inorder,0,len-1);
}
public TreeNode createTreeNode(int[] inorder, int[] postorder, int inLeft, int inRight){
if (inLeft == inRight){
TreeNode node = new TreeNode(inorder[inLeft]);
node.left = null;
node.right = null;
return node;
}
int val = postorder[postIndex];
int findIndex = inLeft;
while (findIndex != inRight && val != inorder[findIndex]){
findIndex++;
}
TreeNode leftNode;
TreeNode rightNode;
if (findIndex == inRight){
rightNode = null;
}else{
--postIndex;
rightNode = createTreeNode(inorder,postorder,findIndex+1,inRight);
}
if (findIndex == inLeft){
leftNode = null;
}else{
--postIndex;
leftNode = createTreeNode(inorder,postorder,inLeft,findIndex-1);
}
TreeNode root = new TreeNode(val);
root.left = leftNode;
root.right = rightNode;
return root;
}
}博主算法方面比較薄弱,寫得不好,歡迎大家給我留言哈!!!