UVA 1414 - Hanoi Towers(dp)

The ``Hanoi Towers" puzzle consists of three pegs (that we will name A , B , and C ) with n disks of different diameters stacked onto the pegs. Initially all disks are stacked onto peg A with the smallest disk at the top and the largest one at the bottom, so that they form a conical shape on peg A .

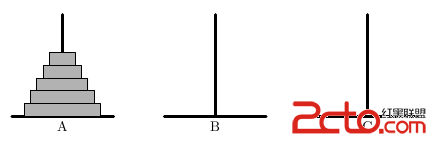
A valid move in the puzzle is moving one disk from the top of one (source) peg to the top of the other (destination) peg, with a constraint that a disk can be placed only onto an empty destination peg or onto a disk of a larger diameter. We denote a move with two capital letters - the first letter denotes the source disk, and the second letter denotes the destination disk. For example, AB is a move from disk A to disk B .

The puzzle is considered solved when all the disks are stacked onto either peg B (with pegs A and C empty) or onto peg C (with pegs A and B empty). We will solve this puzzle with the following algorithm.

All six potential moves in the game (AB, AC, BA, BC, CA, and CB) are arranged into a list. The order of moves in this list defines our strategy. We always make the first valid move from this list with an additional constraint that we never move the same disk twice in a row.

It can be proven that this algorithm always solves the puzzle. Your problem is to find the number of moves it takes for this algorithm to solve the puzzle using a given strategy.

Input

Input contains several dataset. Each dataset contains two lines. The first line consists of a single integer number n (1n30) -- the number of disks in the puzzle. The second line contains descriptions of six moves separated by spaces - the strategy that is used to solve the puzzle.

Output

For each dataset, write to the output file the number of moves it takes to solve the puzzle. This number will not exceed 10¹⁸ .

Sample Input

3 
AB BC CA BA CB AC 
2 
AB BA CA BC CB AC

Sample Output

7 
5

題意：3個樁的漢諾塔，n個盤子，所有盤子起先都是在 A 上，給一個列表，6個成對的字母，表示移動方式，從頭開始走那個表，找到第一個可以移動的方去移動，然後就退出，又從頭開始走第二遍表。這裡還有另外一個條件，就是同一個盤子不能被連續的移動兩次，最後讓你輸出步數。

思路：沒推出來，看了別人題解，居然是去設 f[i] = f[i - 1] * x + y；然後利用模擬求前3項，然後就能求出x，y，然後遞推即可。

代碼：

#include 
#include 
#include 
using namespace std;

int n, i;
long long f[35], x, y;
char str[6][3];

long long get(int n) {
	long long ans = 0;
	int fa = -1;
	stack h[3];
	for (int i = n; i >= 1; i--)
		h[0].push(i);
	while (1) {
		for (int i = 0; i < 6; i++) {
			int s = str[i][0] - 'A', e = str[i][1] - 'A';
			if (!h[s].empty() && h[s].top() != fa && (h[e].empty() || h[s].top() < h[e].top())) {
				fa = h[s].top();
				h[e].push(h[s].top());
				h[s].pop();
				ans++;
				break;
			}
		}
		if (h[1].size() == n || h[2].size() == n)
			return ans;
	}
}

long long solve() {
	for (i = 1; i <= 3; i++)
		f[i] = get(i);
	x = (f[2] - f[3]) / (f[1] - f[2]);
	y = f[2] - x * f[1];
	for (i = 4; i <= n; i++) {
		f[i] = x * f[i - 1] + y;
	}
	return f[n];
}

int main() {
	while (~scanf("%d", &n)) {
		for (int i = 0; i < 6; i++)
			scanf("%s", str[i]);
		printf("%lld\n", solve());
	}
	return 0;
}