昨晚做了九度oj上的練習賽。。
讓我感覺這些題目對於acm來說真是心不難。。
好了,閒話少說,就給出最後兩道的題解。
時間限制:1 秒
內存限制:128 兆
特殊判題:否
提交:236
解決:71
有如下圖半價為R的圓形蛋糕,被切一刀後(圖中紅色直線),分成兩個部分(黃色和綠色),已知其比例為r,求刀痕長度(圖中紅色直線)。
輸入包括多組測試數據,包括一個整數R(1<=R<=1000),和一個浮點數r(0
對於每組測試用例,輸出一個浮點數,代表刀痕的長度,保留二位小數。
首先是要靠你一步一步推出公式 假設半徑為R,比例為f S為圓的面積 q為切線交點和圓心的連線的角度的一半 然後可知切割後的一部分面積為x = (f*S)/(f+1) 然後R^2*q - R^2*sin(2*q)/2 = x 對於這條方程最主要就是求出q的值,但是~~我不會 所以我就用最簡單的方法求:二分求值 然後ans = 2.0*R*sin(mid)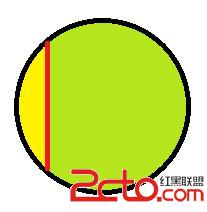
1000 0.5000
500 0.6183
1928.53
982.49
#include
————————————————————————————————————————————————————————————
————————————————————————————————————————————————————————————
時間限制:1 秒
內存限制:128 兆
特殊判題:否
提交:227
解決:60
計算機學院的男生和女生共n個人要坐成一排玩游戲,因為計算機的女生都非常害羞,男生又很主動,所以活動的組織者要求在任何時候,一個女生的左邊或者右邊至少有一個女生,即每個女生均不會只與男生相鄰。現在活動的組織者想知道,共有多少種可選的座位方案。
例如當n為4時,共有
女女女女, 女女女男, 男女女女, 女女男男, 男女女男, 男男女女, 男男男男
7種。
輸入包含多組測試用例,每組測試用例僅包含一個整數n(1<=n<=1000)。
對於每組測試用例,輸出一個數代表可選的方案數,為防止答案過大,答案對1000000007取模。
1 2 4
1 2 7
不過哥狀態方程我也想了很久,丟臉!~~~
dp[i][j]表示第i個放男和女的個數(j為0是男,j為1是女)
然後很容易dp[i][0] = dp[i-1][0]+dp[i-1][1];
關鍵就是dp[i][1]這麼表示
其實dp[i][1] = sum(dp[k][0])(k = 0~i-2)
其實意思就是最後一個放女的那倒數第二個就一定也是女的但是男的最後一個放在那裡呢
就是枚舉最後一個男的位置
把所有的情況都考慮了一遍
這個操作可以用單調隊列來實現
最後時間復雜度就變成裡O(n)
#include#include #include #include #include #include using namespace std; #define MOD 1000000007 int dp[1005][3]; void Init() { int i,j; memset(dp,0,sizeof(dp)); dp[1][0] = 1; dp[1][1] = 0; dp[0][0] = 1; //dp[2][] int sum = 0; for(i=2;i<1003;i++) { dp[i][0] = (dp[i-1][0]+dp[i-1][1])%MOD; sum = (sum+dp[i-2][0])%MOD; dp[i][1]=(dp[i][1]+sum)%MOD; } } int main() { int n,i,j; Init(); while(~scanf("%d",&n)) { printf("%d\n",(dp[n][0]+dp[n][1])%MOD); } return 0; }