九度OJ 1541 二叉樹[數據結構]

旋轉是二叉樹的基本操作，我們可以對任意一個存在父親節點的子節點進行旋轉，包括如下幾種形式（設被旋轉節點為x，其父親節點為p）：
1.左旋
旋轉前，x是p的右兒子。
x的左兒子（若存在）變為p的右兒子，p變為x的左兒子。如下圖

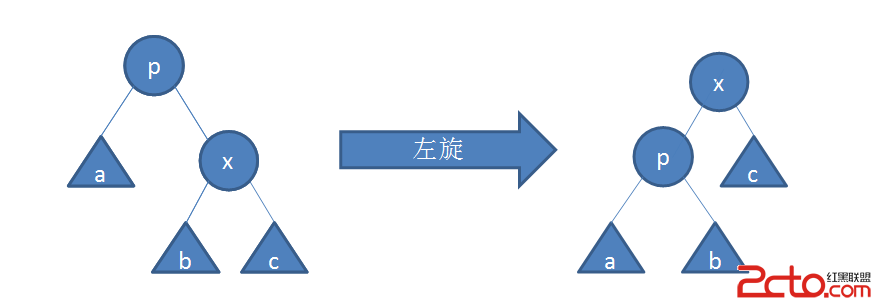
2.右旋
旋轉前，x是p的左兒子。
x的右兒子（若存在）變為p的左兒子，p變為x的右兒子。如下圖

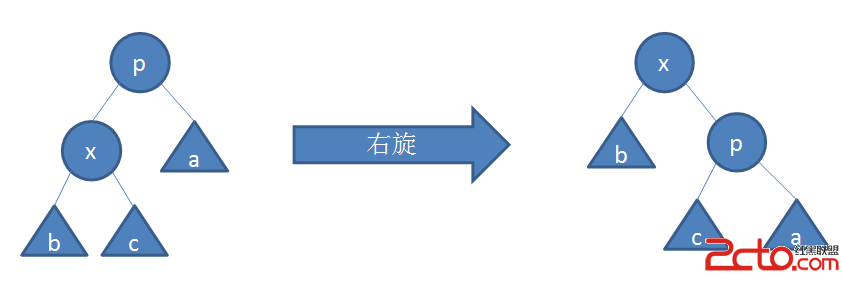
綜上，我們可以通過檢查選擇前x是p的左兒子還是右兒子來判斷該次旋轉是左旋還是右旋。

給定一顆n個節點的二叉樹，其節點由1至n編號，並給定一系列操作，如下：
1.rotate x，對編號x的節點進行旋轉，若x為根節點，則不進行任何操作。
2.parent x，輸出編號x的父親節點編號，若x為根節點輸出-1。
3.size x，輸出以x為根節點的子樹的節點個數。

輸入：

輸入包含多組測試用例。
每組測試用例開頭為一個整數n（1<=n<=1000），代表二叉樹的節點個數。
接下去n行描述，二叉樹原始的狀態，第i行為兩個整數x，y，代表i號節點的左兒子節點為x號節點，右兒子節點為y號節點，若x或y為-1，則表示相應兒子節點不存在。編號的范圍為1到n。
接下去一行為一個整數t(1<=t<=50000)，代表操作的個數。
最後t行，每行代表一個對二叉樹的操作，描述如上所示。

 

輸出：

對於每組測試用例，輸出操作parent x和size x查詢的數據。

 

樣例輸入：

5
2 3
-1 -1
4 5
-1 -1
-1 -1
5
size 1
rotate 5
size 5
parent 3
parent 4

樣例輸出：

5
3
5
3

 

 

#include 
#include 
 
typedef struct node{
    int parent;
    int left;
    int right;
}Node;
 
Node tree[1001];
int has_parent[1001];
int size[1001];
int n;
int root;
 
int Compute(int node){
    return (node == -1) ? 0 : size[node];
}
 
int Size(int node){
    if (node == -1)
        return 0;
    if (tree[node].left != -1)
        size[tree[node].left] = Size(tree[node].left);
    if (tree[node].right != -1)
        size[tree[node].right] = Size(tree[node].right);
    return size[node] = Compute(tree[node].left) + Compute(tree[node].right) + 1; 
}
 
void Rotate(int node){
    int parent, grandpar;
    int left, right;
    if (node != root){
        parent = tree[node].parent;
        grandpar = tree[parent].parent;
        tree[node].parent = grandpar;
        if (grandpar != -1){
            if (tree[grandpar].right == parent)
                tree[grandpar].right = node;
            else
                tree[grandpar].left = node;
        }
        if (parent == root)
            root = node;
        tree[parent].parent = node;
        if (tree[parent].right == node){//node是其父節點的右孩子，左旋 
            left = tree[node].left;
            tree[parent].right = left;
            tree[node].left = parent;
            if (left != -1){
                tree[left].parent = parent;
            }
        }
        else{//node是其父節點的左孩子，右旋 
            right = tree[node].right;
            tree[parent].left = right;
            tree[node].right = parent;
            if (right != -1){
                tree[right].parent = parent;
            }
        }
        size[node] = size[parent];
        size[parent] = Compute(tree[parent].left) + Compute(tree[parent].right) + 1;
    }
}
 
int main(void) {
    int i;
    int t;
    char ope[10];
    int id;
     
    while (scanf(%d, &n) != EOF){
        for (i = 1; i <= n; ++i){
            memset(has_parent, 0, sizeof(has_parent));
            memset(size, 0, sizeof(size));
            scanf(%d%d, &tree[i].left, &tree[i].right);
            if (tree[i].left != -1){
                tree[tree[i].left].parent = i;
                has_parent[tree[i].left] = 1;
            }   
            if (tree[i].right != -1){
                tree[tree[i].right].parent = i;
                has_parent[tree[i].right] = 1;
            }
        }
        for (i = 1; i <= n; ++i)
            if (has_parent[i] != 1){
                tree[i].parent = -1;
                root = i;
                break;
            }
        for (i = 1; i <= n; ++i)
            Size(i);
        scanf(%d, &t);
        while (t-- != 0){
            scanf(%s%d, ope, &id);
            if (ope[0] == 'r')
                Rotate(id);
            else if (ope[0] == 'p')
                printf(%d
, tree[id].parent);
            else
                printf(%d
, size[id]);
        }
    }
     
    return 0;
}