高快省的排序算法
有沒有既不浪費空間又可以快一點的排序算法呢?那就是“快速排序”啦!光聽這個名字是不是就覺得很高端呢。
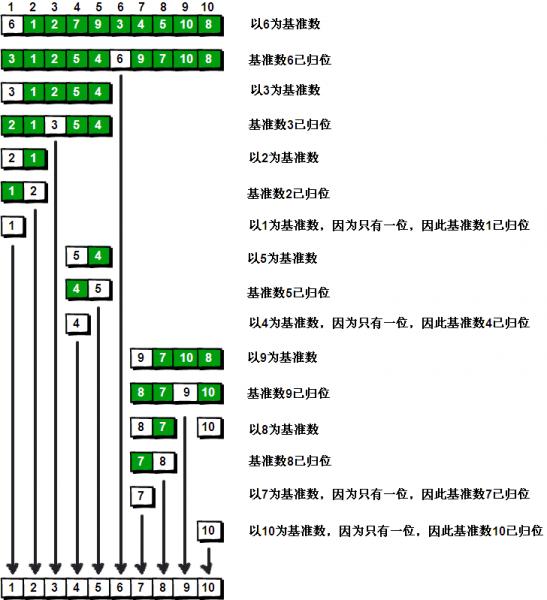
假設我們現在對“6 1 2 7 9 3 4 5 10 8”這個10個數進行排序。首先在這個序列中隨便找一個數作為基准數不要被這個名詞嚇到了,就是一個用來參照的數,待會你就知道它用來做啥的了)。為了方便,就讓第一個數6作為基准數吧。接下來,需要將這個序列中所有比基准數大的數放在6的右邊,比基准數小的數放在6的左邊,類似下面這種排列:
3 1 2 5 4 6 9 7 10 8
在初始狀態下,數字6在序列的第1位。我們的目標是將6挪到序列中間的某個位置,假設這個位置是k。現在就需要尋找這個k,並且以第k位為分界點,左邊的數都小於等於6,右邊的數都大於等於6。想一想,你有辦法可以做到這點嗎?
排序算法顯神威
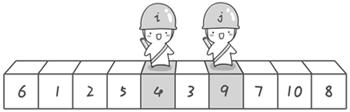
方法其實很簡單:分別從初始序列“6 1 2 7 9 3 4 5 10 8”兩端開始“探測”。先從右往左找一個小於6的數,再從左往右找一個大於6的數,然後交換他們。這裡可以用兩個變量i和j,分別指向序列最左邊和最右邊。我們為這兩個變量起個好聽的名字“哨兵i”和“哨兵j”。剛開始的時候讓哨兵i指向序列的最左邊即i=1),指向數字6。讓哨兵j指向序列的最右邊即=10),指向數字。
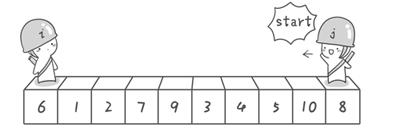
首先哨兵j開始出動。因為此處設置的基准數是最左邊的數,所以需要讓哨兵j先出動,這一點非常重要請自己想一想為什麼)。哨兵j一步一步地向左挪動即j--),直到找到一個小於6的數停下來。接下來哨兵i再一步一步向右挪動即i++),直到找到一個數大於6的數停下來。最後哨兵j停在了數字5面前,哨兵i停在了數字7面前。
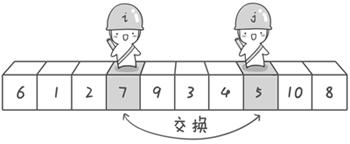
現在交換哨兵i和哨兵j所指向的元素的值。交換之後的序列如下:
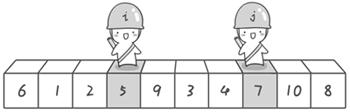
6 1 2 5 9 3 4 7 10 8
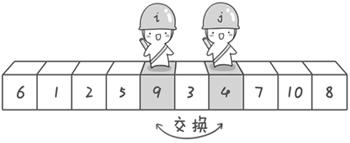
到此,第一次交換結束。接下來開始哨兵j繼續向左挪動再友情提醒,每次必須是哨兵j先出發)。他發現了4比基准數6要小,滿足要求)之後停了下來。哨兵i也繼續向右挪動的,他發現了9比基准數6要大,滿足要求)之後停了下來。此時再次進行交換,交換之後的序列如下:
6 1 2 5 4 3 9 7 10 8
第二次交換結束,“探測”繼續。哨兵j繼續向左挪動,他發現了3比基准數6要小,滿足要求)之後又停了下來。哨兵i繼續向右移動,糟啦!此時哨兵i和哨兵j相遇了,哨兵i和哨兵j都走到3面前。說明此時“探測”結束。我們將基准數6和3進行交換。交換之後的序列如下:
3 1 2 5 4 6 9 7 10 8
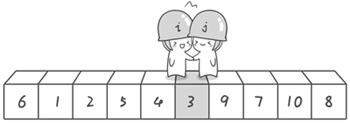
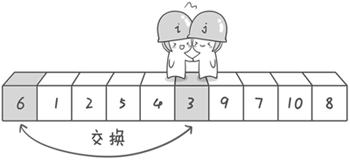
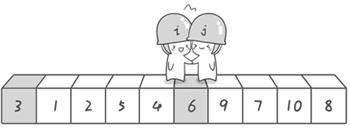
到此第一輪“探測”真正結束。此時以基准數6為分界點,6左邊的數都小於等於6,6右邊的數都大於等於6。回顧一下剛才的過程,其實哨兵j的使命就是要找小於基准數的數,而哨兵i的使命就是要找大於基准數的數,直到i和j碰頭為止。
OK,解釋完畢。現在基准數6已經歸位,它正好處在序列的第6位。此時我們已經將原來的序列,以6為分界點拆分成了兩個序列,左邊的序列是“3 1 2 5 4”,右邊的序列是“9 7 10 8”。接下來還需要分別處理這兩個序列。因為6左邊和右邊的序列目前都還是很混亂的。不過不要緊,我們已經掌握了方法,接下來只要模擬剛才的方法分別處理6左邊和右邊的序列即可。現在先來處理6左邊的序列現吧。
左邊的序列是“3 1 2 5 4”。請將這個序列以3為基准數進行調整,使得3左邊的數都小於等於3,3右邊的數都大於等於3。好了開始動筆吧
如果你模擬的沒有錯,調整完畢之後的序列的順序應該是:
2 1 3 5 4
OK,現在3已經歸位。接下來需要處理3左邊的序列“2 1”和右邊的序列“5 4”。對序列“2 1”以2為基准數進行調整,處理完畢之後的序列為“1 2”,到此2已經歸位。序列“1”只有一個數,也不需要進行任何處理。至此我們對序列“2 1”已全部處理完畢,得到序列是“1 2”。序列“5 4”的處理也仿照此方法,最後得到的序列如下:
1 2 3 4 5 6 9 7 10 8
對於序列“9 7 10 8”也模擬剛才的過程,直到不可拆分出新的子序列為止。最終將會得到這樣的序列,如下
1 2 3 4 5 6 7 8 9 10
到此,排序完全結束。細心的同學可能已經發現,快速排序的每一輪處理其實就是將這一輪的基准數歸位,直到所有的數都歸位為止,排序就結束了。下面上個霸氣的圖來描述下整個算法的處理過程。
這是為什麼呢?
快速排序之所比較快,因為相比冒泡排序,每次交換是跳躍式的。每次排序的時候設置一個基准點,將小於等於基准點的數全部放到基准點的左邊,將大於等於基准點的數全部放到基准點的右邊。這樣在每次交換的時候就不會像冒泡排序一樣每次只能在相鄰的數之間進行交換,交換的距離就大的多了。因此總的比較和交換次數就少了,速度自然就提高了。當然在最壞的情況下,仍可能是相鄰的兩個數進行了交換。因此快速排序的最差時間復雜度和冒泡排序是一樣的都是O(N2),它的平均時間復雜度為O(NlogN)。其實快速排序是基於一種叫做“二分”的思想。我們後面還會遇到“二分”思想,到時候再聊。先上代碼,如下
可以輸入以下數據進行驗證
- #include <stdio.h>
- int a[101],n;//定義全局變量,這兩個變量需要在子函數中使用
- void quicksort(int left,int right)
- {
- int i,j,t,temp;
- if(left>right)
- return;
- temp=a[left]; //temp中存的就是基准數
- i=left;
- j=right;
- while(i!=j)
- {
- //順序很重要,要先從右邊開始找
- while(a[j]>=temp && i<j)
- j--;
- //再找右邊的
- while(a[i]<=temp && i<j)
- i++;
- //交換兩個數在數組中的位置
- if(i<j)
- {
- t=a[i];
- a[i]=a[j];
- a[j]=t;
- }
- }
- //最終將基准數歸位
- a[left]=a[i];
- a[i]=temp;
- quicksort(left,i-1);//繼續處理左邊的,這裡是一個遞歸的過程
- quicksort(i+1,right);//繼續處理右邊的 ,這裡是一個遞歸的過程
- }
- int main()
- {
- int i,j,t;
- //讀入數據
- scanf("%d",&n);
- for(i=1;i<=n;i++)
- scanf("%d",&a[i]);
- quicksort(1,n); //快速排序調用
- //輸出排序後的結果
- for(i=1;i<=n;i++)
- printf("%d ",a[i]);
- getchar();getchar();
- return 0;
- }
1061279345108
運行結果是
12345678910
漲姿勢環節
快速排序由 C. A. R. Hoare東尼霍爾,Charles Antony Richard Hoare)在1960年提出,之後又有許多人做了進一步的優化。如果你對快速排序感興趣可以去看看東尼霍爾1962年在Computer Journal發表的論文“Quicksort”以及《算法導論》的第七章。快速排序算法僅僅是東尼霍爾在計算機領域才能的第一次顯露,後來他受到了老板的賞識和重用,公司希望他為新機器設計一個新的高級語言。你要知道當時還沒有PASCAL或者C語言這些高級的東東。後來東尼霍爾參加了由Edsger Wybe Dijkstra1972年圖靈獎得主,這個大神我們後面還會遇到的到時候再細聊)舉辦的“ALGOL 60”培訓班,他覺得自己與其沒有把握去設計一個新的語言,還不如對現有的“ALGOL 60”進行改進,使之能在公司的新機器上使用。於是他便設計了“ALGOL 60”的一個子集版本。這個版本在執行效率和可靠性上都在當時“ALGOL 60”的各種版本中首屈一指,因此東尼霍爾受到了國際學術界的重視。後來他在“ALGOL X”的設計中還發明了大家熟知的“case”語句,後來也被各種高級語言廣泛采用,比如PASCAL、C、Java語言等等。當然,東尼霍爾在計算機領域的貢獻還有很多很多,他在1980年獲得了圖靈獎。
更多算法教程,請移步:
http://ahalei.blog.51cto.com/