題目:斐波那契數列,FIBONACCI數列特點是第1,第2兩個數為1,1.從第3個數開始,該數是前兩個數之和,求這個數列的前30個元素
分析: 費波那西數列(Fibonacci Sequence),又譯費波拿契數、斐波那契數列、費氏數列、黃金分割數列。在數學上,費波那西數列是以遞歸的方法來定義:
F0 = 0
F1 = 1
Fn = Fn- 1 + Fn - 2
用文字來說,就是費波那西數列由 0 和 1 開始,之後的費波那西係數就由之前的兩數相加。首幾個費波那西係數是(OEIS A000045):
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584,
4181, 6765, 10946,………………
特別指出:0不是第一項,而是第零項。(參考)
分析題目我們可以用如下等式來表示斐波那契數列:
F1=1----(n=1);
F2=1----(n=1);
Fn=F(n-1)+F(n-2)-----(n>=3)
這裡我們將F的下標看成是數組的下標代碼如下:
#include<stdio.h>#include<stdlib.h>int main(){ int i;/*定義整形變量*/ long f[31];/*定義數組為長整形*/ f[1]=f[2]=1;/*數組的f[1],f[2]賦值為1*/ for(int i=3;i<31;i++) { f[i]=f[i-1]+f[i-2];/*數組從第三行開始,每一項等於前兩項之和*/ } for(i=1;i<31;i++) { printf("%10ld",f[i]);/*輸出數組中的30個元素*/ if(i%5==0) printf("
");/*每5個元素進行一次換行*/ } system("PAUSE"); }
結果:

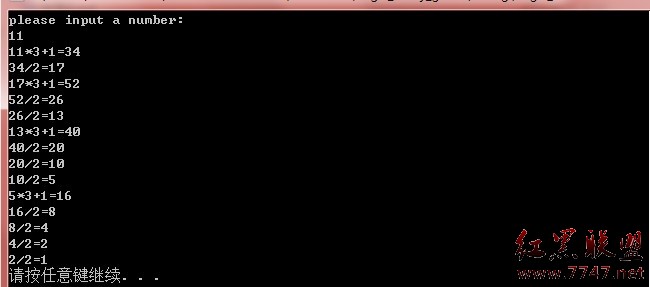
題目:角谷猜想 ,任意一個自然數,當他為偶數的時候則除以2,當他為奇數的時候則乘3加1,得到一個新的自然數,依次按照這個法則繼續演算,到很多次以後,就會得到一個結果,這個結果是1...
分析:考拉茲猜想,又稱為3n+1猜想、冰雹猜想、角谷猜想、哈塞猜想、烏拉姆猜想或敘拉古猜想,是指對於每一個正整數,如果它是奇數,則對它乘3再加1,如果它是偶數,則對它除以2,如此循環,最終都能夠得到1。(維基百科)
有題目分析可知,重點是判斷一個數是奇數還是偶數,程序采用對2取余的方法,當余數為0時,說明該數為偶數,否則為奇數
舉例:取一個數字
如n = 6,根據上述數式,得出 6→3→10→5→16→8→4→2→1 。(步驟中最高的數是16,共有7個步驟)
如n = 11,根據上述數式,得出 11→34→17→52→26→13→40→20→10→5→16→8→4→2→1。(步驟中最高的數是40,共有13個步驟)
如n = 27,根據上述數式,得出 : 27→82→41→124→62→31→94→47→142→71→214→107→322→161→484→242→121→364→182→91→274→137→412→206→103→310→155→466→233
→700→350→175→526→263→790→395→1186→593→1780→890→445→1336→668→334→167→502→251→754→377→1132→566→283→850→425→1276
→638→319→958→479→1438→719→2158→1079→3238→1619→4858→2429→7288→3644→1822→911→2734→1367→4102→2051→6154→3077→9232
→4616→2308→1154→577→1732→866→433→1300→650→325→976→488→244→122→61→184→92→46→23→70→35→106→53→160→80→40→20→10
→5→16→8→4→2→1。(步驟中最高的數是9232,共有111個步驟)
考拉茲猜想稱,任何正整數,經過上述計算步驟後,最終都會得到 1 。代碼:
#include<stdio.h>#include<stdlib.h>void main(){ long i,n; //定義變量為長整形 printf("please input a number:
");//輸入任意一個長整形數 scanf("%ld",&n); while(n!=1) { if(n%2==0) //判斷是否為偶數 { printf("%ld/2=%ld
",n,n/2);//當為偶數的時候n除以2 n=n/2; } else { printf("%ld*3+1=%ld
",n,n*3+1);//當我奇數時乘以3加1 n=n*3+1; } } system("pause");}
結果:
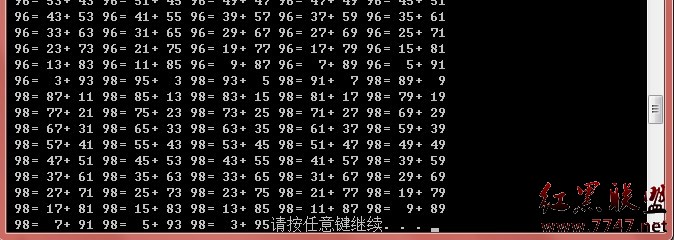
題目:歌德巴赫猜想,驗證100以內的的正偶數都能分解為兩個素數之和
分析:任一大於2的偶數,都可表示成兩個質數之和。
將一給定的偶數表示成兩個質數之和被稱之為此數的哥德巴赫分割。例如,
4 = 2 + 2
6 = 3 + 3
8 = 3 + 5
10 = 3 + 7 = 5 + 5
12 = 5 + 7
14 = 3 + 11 = 7 + 7
…
換句話說,哥德巴赫猜想主張每個大於等於4的偶數都是哥德巴赫數-可表示成兩個質數之和的數[1]。哥德巴赫猜想也是希爾伯特第八問題中的一個子問題。
另有對奇數的相似猜想,稱之為勒穆瓦納猜想(Lemoines conjecture)或李維猜想(Levys conjecture)。
為了驗證哥德巴赫猜想對100以內的正偶數成立,所以要將正偶數分為兩部分,在對這兩部分進行判斷,如果均是素數則滿足體藝,不是的話,則重新分解繼續判斷代碼:
#include<stdio.h>#include<stdlib.h> int ss(int i)/*自定義一個函數是不是素數*/ { int j; if(i<=1)/*小於1的不是素數*/ return 0; if(i==2) /*2是素數*/ return 1; for(j=2;j<i;j++)/*對大於2的進行判斷*/ { if(i%j==0) return 0; else if(i!=j+1) return 1; } } void main() { int i,j,k,flag1,flag2,n=0; for(i=6;i<100;i+=2) for(k=2;k<=i;k++) { j=i-k; flag1=ss(k); if(flag1) /*判斷拆分的數是不是素數*/ { flag2=ss(j); if(flag2) /*如果拆分出來的數是素數則輸出*/ { printf("%3d=%3d+%3d",i,j,k); n++; if(n%5==0) printf("
"); } } } system("pause"); } 結果:
題目:四方定理,所有的自然數至多只要4個數的平方和就可以表示,編程驗證
可以采用窮舉試探的方法進行計算,當滿足定理的條件就可以輸出結果
代碼:
#include<stdio.h>#include<stdlib.h>int main(){ long i,j,k,l,n;//定義變量為長整形 printf("請輸入 一個長整形的整數"); scanf("%ld",&n); for(i=0;i<n;i++) //對i,j,k,l進行窮舉 for(j=0;j<i;j++) for(k=0;k<j;k++)