一、需求分析
在數據結構中,樹有兩種存儲方式,一種是鏈式存儲,另一種是順序存儲。前者就是使用指針來記錄樹結點間的關系,在新增結點或刪除結點時,只需改變與父結點或兄弟結點的指針值即可,實現較為簡單;後者就是使用數組來存儲,可以用相對偏移量來記錄樹結點間的關系,在新增結點或刪除結點時,則不僅是改變與父結點或兄弟結點的相對偏移量,還需要改變其它結點的相對偏移量,實現較為復雜。近來在項目中,對一個普通文本文件進行分析提取數據,而這個文件內的數據從內容看,具有層次嵌套關系,要將這樣的數據發送到服務器去處理,我考慮了兩種如下方法:
(1)自定義XML格式,在本地使用XML庫,如libxml2、tinyxml等,將數據寫到XML臨時文件或內存中,再將這個XML臨時文件或內存發過去,在服務器那邊使用XML庫來解析。這種方法比較通用而且跨平台,如果XML庫不支持將其所存儲的數據轉儲到一塊連續內存,那麼就只能先存到XML臨時文件,再將這個文件發過去,這樣一來,就存在磁盤IO操作,效率較低。否則,就可以先將數據轉儲到一塊連續內存,再將這塊內存發過去,這樣一來,這塊連續內存就需要另外開辟,因此多了一套內存管理操作,但是比用臨時文件方式,沒有磁盤IO,效率要高些。
(2)實現基於順序存儲的樹,而且還是多叉樹,因為實際數據具有多層次嵌套關系,將數據放進這顆樹中,再直接將這顆樹發過去,在服務器那邊直接解析這顆樹,這樣一來,不用臨時文件,沒有磁盤IO,無須另外開辟內存,充分利有現有空間,效率較高。
二、設計開發
從服務器效率至上的觀點考慮,我選擇了第2種方法,因此就自已實現了基於順序存儲的多叉樹,關於順序存儲,又有兩種如下方式:
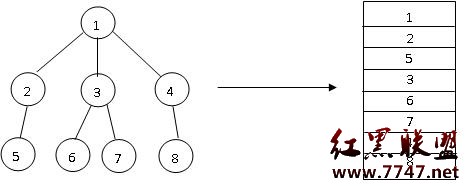
(1)深度優先存儲,按照自上而下從左到右存儲樹的所有結點,先存儲結點及它的孩子,再存儲它的兄弟。因此結點的孩子和兄弟都不一定是連續的,當一個結點的所有孩子都是葉子結點時,則所有孩子是連續存放的。結點和它的第一個孩子(若有)是連續的,如下圖所示
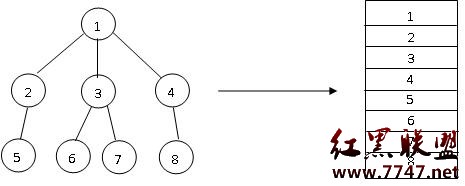
(2)廣度優先存儲,按照從左到右自上而下存儲樹的所有結點,先存儲結點及它的兄弟,再存儲它的孩子,因此結點的孩子和兄弟都是連續存放的,孩子與其父親之間不一定是連續的,如下圖所示
本文描述第1種存儲方式實現的多叉樹,介紹三種主要操作:設置根結點、增加結點和刪除結點,為簡單起見,使用vector作為內部動態數組,使用索引而非迭代器作為外部接口,來訪問結點,索引0表示空索引,有效索引從1開始。關於迭代器的設計,有諸多考慮,如前序、後序、廣度優先、指定深度、葉子結點等各種遍歷方法,因時間和篇幅原因,不能一一講述,待後面有時間會陸續補充完善。
1)樹結點定義,由5個偏移量域和1個數據域組成,C++代碼描述如下
1template <typename T>
2struct tree_node
3{
4 //結點相對偏移量,即相對於自己的距離,值為非負數,0表示沒有
5 size_t parent; //父結點偏移量
6 size_t first_child; //第一個孩子結點偏移量
7 size_t last_child; //最後一個孩子結點偏移量
8 size_t prev_sibling; //前一個左兄弟結點偏移量
9 size_t next_sibling; //後一個右兄弟結點偏移量
10 T data; //實際存儲的數據
11
12 tree_node()
13 {
14 }
15
16 tree_node(const T& _data)
17 :parent(0)
18 ,first_child(0)
19 ,last_child(0)
20 ,prev_sibling(0)
21 ,next_sibling(0)
22 ,data(_data)
23 {
24 }
25};
2)設置根結點,為方便實現,根結點固定存放在數組中第1個位置,對應內部下標為0,外部索引為1,C++代碼描述如下
1template<typename T>
2void mtree::set_root(const T& val)
3{
4 if (m_nodes.empty())
5 {
6 //增加根結點
7 tree_node node(val);
8 m_nodes.push_back(node);
9 }
10 else
11 {
12 //修改根結點的數據
13 tree_node& node = m_nodes[0];
14 node.data = val;
15 }
16}
3)增加結點,這裡要分為三步,第一步要找到插入位置,第二步插入結點,第三步改變相關結點的相對偏移量,這裡相關結點包括當前所插結點、所插結點兄弟結點、父結點、祖先結點及其右兄弟結點;注意,這裡可以作一些異常安全考慮,即如果第二步操作失敗了,則可直接返回,這樣就可保證整顆樹不受影響。為了簡單起見,以下C++代碼對異常安全沒有作處理,描述如下
1template<typename T>
2size_t mtree::append_child(size_t index,const T& val)
3{
4 assert(index>=1 && index<=size());
5 size_t parent = index, pos;
6 tree_node<T> *p_parent = &m_nodes[parent-1],*p_link, *p_child;
7
8 //找到插入位置
9 pos = parent; p_link = p_parent;
10 while (p_link->last_child)
11 {
12 pos += p_link->last_child;
13 p_link = &m_nodes[pos-1];
14 }
15 size_t child = ++pos;
16 //插入結點
17 tree_node<T> node(val);
18 if (child > size())
19 m_nodes.push_back(node);
20 else
21 m_nodes.insert(m_nodes.begin()+child-1,node);
22
23 //更新當前結點的prev_sibling值和其左兄弟結點的next_sibling值
24 p_child = &m_nodes[child-1];
25 p_parent = &m_nodes[parent-1];
26 if (p_parent->last_child)
27 {
28 pos = parent+p_parent->last_child;
29 m_nodes[pos-1].next_sibling = p_child->prev_sibling = child-pos;
30 }
31 //從父結點開始,向上更新當前結點所有右邊結點的偏移量
32 size_t next;
33 tree_node<T>* p_next;
34 pos = parent;
35 do
36 {
37 p_link = &m_nodes[pos-1];
38 if (p_link->next_sibling)
39 {
40 if (p_link->parent)
41 ++m_nodes[pos-p_link->parent-1].last_child;
42 //更新其祖先結點的next_sibling值
43 ++p_link->