1.set的宣言
先看看C++標准中對set的介紹:
A set is a kind of associative container that supports unique keys (contains at most one
of each key value) and provides for fast retrieval of the keys themselves. Set supports
bidirectional iterators
下面列舉關於set的兩點事實,需要注意:
set對於性能有明確的保證:set::find和set::insert消耗時間級別都為logN。所以,如果你確實需要保證插入和檢索時間在logN,set可能是個不錯的選擇。
set底層實現通常使用red-black tree:有額外的空間和時間負擔。每個red-black tree的節點都需要存儲顏色標記、指向子女和父親的指針;插入需要樹的重新平衡;查詢和遍歷需要指針操作。
2.另外的選擇:二分查找
紅黑樹並非提供logN級別的搜索的唯一數據結構。很容易想到的就是在有序數集中進行binary_search,該算也提供的logN級別的時間復雜度,而且最數據結構的要求僅僅是“一個有序順序集(該集支持某些必要操作)”,而且, 常數因子比set更小。使用set會占用更多的空間,不利於cache機制的使用,且可能造成更多的page faults。
事實勝於雄辯,下面是用一段代碼來對比set提供的搜索和二分查找提供的搜索的性能,編譯環境為WOW64 Release
注意: 檢測元素是否搜索到是必須的,此處忽略之,對於push_back等的調用其實可以使用“范圍函數”來完成,可能性能更好!
#include <iostream>
#include <set>
#include <vector>
#include <algorithm>
#include <windows.h>
int main()
{
using namespace std;
const int MAX_ELEMENT = 1000000;
const int MAX_SIZE = MAX_ELEMENT+1;
const int MAX_TIMES = 10000000;
set<int> intSet;
vector<int> intVect;
intVect.reserve(MAX_SIZE);
for (int i = 0; i < MAX_SIZE; ++i)
{
intSet.insert(i);
intVect.push_back(i); //這裡由於插入的特殊性,intVect元素狀態是“有序”的
}
DWORD st1, st2;
st1 = GetTickCount();
for (int i = 0; i < MAX_TIMES; ++i)
{
intSet.find(MAX_ELEMENT);
intSet.find(MAX_ELEMENT/2);
intSet.find(MAX_ELEMENT/15);
}
st2 = GetTickCount();
cout << "intSet.find(...):\t" << (st2 - st1) << "ms" << endl;
st1 = GetTickCount();
for (int i = 0; i < MAX_TIMES; ++i)
{
binary_search(intVect.begin(), intVect.end(), MAX_ELEMENT);
binary_search(intVect.begin(), intVect.end(), MAX_ELEMENT/2);
binary_search(intVect.begin(), intVect.end(), MAX_ELEMENT/15);
}
st2 = GetTickCount();
cout << "binary_search(...):\t" << (st2 - st1) << "ms" << endl;
return 0;
}
運行截圖:
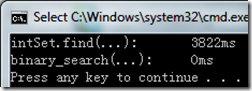
可以看到,由於緩存、缺頁等各方面因素,二分查找和對於set的查找性能相差極大。更詳細的信息可以用Profiler來獲得。下面給出了任務管理器中的截圖,程序為STL.exe*32。
![]()
3.總結,3個選擇
1.使用set:當元素個數可能會變得足夠大,即N足夠大,logN和N的區別非常明顯之時,元素是隨機插入的,插入和搜索交互發生,無法預料下一次的操作。
2.使用sorted_vector:需要快速的搜索和遍歷,但是對插入的性能要求很低,或者元素是預先一次性插入的,然後排序好, 在此基礎上進行二分搜索。亦或者對內存限制較大。或者確信搜索操作和插入、刪除操作幾乎不交錯在一起。或者元素的插入是“幾乎有序”的,這樣的插入的額外負擔較小。
3.使用基於哈希表的set:如果哈希函數足夠好和哈希表大小適合,通常情況下會提供常數級別的搜索。
4.簡單sorted_vector實現
#pragma once
#include <vector>
#include <algorithm>
#include <functional>
template <typename T, typename Pred = std::less<T> > class sorted_vector
{
public:
typedef typename std::vector<T>::iterator iterator;
typedef typename std::vector<T>::const_iterator const_iterator;
typedef typename std::vector<T>::size_type size_type;
iterator begin() { return sort_vect.begin(); }
const_iterator begin() const { return sort_vect.cbegin(); }
iterator end() { return sort_vect.end(); }
const_iterator end() const { return sort_vect.cend(); }
void reserve(size_type sz) { sort_vect.reserve(sz); }
//Other wrapper help methods
//...
//Well, use res_size to avoid reallocation possibly
sorted_vector(int res_size, const Pred& p = Pred()) : sort_vect(), pred(p)
{
sort_vect.reserve(res_size);
}
template <typename InputIterator>
sorted_vector(InputIterator first, InputIterator last, const Pred& p = Pred())
: sort_vect(first, last), pred(p)
{
std::sort(begin(), end(), pred);
}
//This container is always sorted
//O(N)
iterator insert(const T& elem)
{
iterator it = std::lower_bound(begin(), end(), elem, pred);
if (it == end() || pred(elem, *it))
sort_vect.insert(it, elem);
return it;
}
//The element is the container should not be modified!!
//O(logN)
const_iterator find(const T& elem) const
{
const_iterator it = lower_bound(begin(), end(), elem, pred);
return it == end() || pred(elem, *it) ? end() : it;
}
private:
std::vector<T> sort_vect;
Pred pred;
};
測試代碼如下,前面的性能比較代碼段中修改即可:
sorted_vector<int> sortVect(MAX_SIZE);
for (int i = 0; i < MAX_SIZE; ++i)
{
intSet.insert(i);
intVect.push_back(i); //這裡由於插入的特殊性,intVect元素狀態是“有序”的
sortVect.insert(i);
}
cout << *(sortVect.find(MAX_ELEMENT/2)) << endl;
DWORD st1, st2;
st1 = GetTickCount();
for (int i = 0; i < MAX_TIMES; ++i)
{
sortVect.find(MAX_ELEMENT);
sortVect.find(MAX_ELEMENT/2);
sortVect.find(MAX_ELEMENT/15);
}
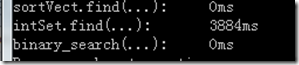
cout << "sortVect.find(...):\t" << (st2 - st1) << "ms" << endl;
運行截圖: