差分約束:線性規劃矩陣A的每一行包含一個1與一個-1,其他元素為0.因此,由Ax<=b給出的約束條件是m個差分約束集合,其中包含n個未知元。每個約束條件為不等式:
xj-xi<=bk
其中1<=i,j<=n,i<=k<=m
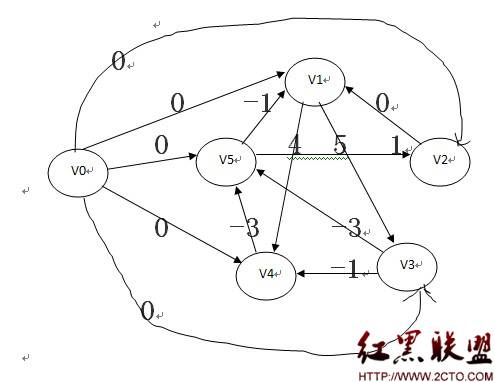
解決方法:把n個未知元看成n的有向圖的頂點,xj-xi<=bk表示頂點j到頂點i長度為bk的有向線段。再添加一個v0頂點,與v0到其余頂點的有向線段,長度為0。(如下圖)
可以證明xi=β(v0,vi)(β(v0,vi)為頂點0到頂點i的最短路徑長度)。所以就可以利用Bellman_Ford算求單源最短路徑(不能用Dijkstra算法,因為有向線段長度可以為負)
// 差分約束系統.cpp : Defines the entry point for the console application.
//
#include "stdafx.h"
#include<iostream>
#define MAX 100
#define Infinity 65535
using namespace std;
//邊的尾節點結構體
struct edgeNode
{
int no; //邊尾端的序號
int weight; //邊權值
struct edgeNode * next; //下一個
};
//節點結構體
struct vexNode
{
char info; //節點名稱
struct edgeNode *link; //與之相連的端點
};
//存儲節點信息
vexNode adjlist[MAX];
//前驅節點
int parent[MAX];
////源點到節點j最短路徑的花費
int lowcost[MAX];
//差分矩陣
int a[MAX][MAX];
//約束集
int w[MAX];
//根據差分矩陣建立鄰接表存儲
//adjlist為節點集,parent[j]為從0節點到節點j的最短路徑的前驅節點
//lowcost[j]為從0節點到節點j的最短路徑的代價
//w為輸入的差分約束
//m,n分別為差分矩陣的行數和列數
void createGraph(vexNode *adjlist,int *parent,int *lowcost,int *w,int m,int n)
{
int i,j;
//初始化,節點vi的名稱為char(a+i)
for(i=0;i<=n;i++)
{
adjlist[i].info = (char)('a' + i);
adjlist[i].link = NULL;
lowcost[i] = Infinity;
parent[i] = i;
}
int col1,col2;
col1 = col2 = 0;
edgeNode *p1;
for(i=1;i<=m;i++)
{
for(j=1;j<=n;j++)
{
if(a[i][j]==-1)
col1 = j;
else if(a[i][j]==1)
col2 = j;
}
p1 = (edgeNode*)malloc(sizeof(edgeNode));
p1->no = col2;
p1->weight = w[i];
p1->next = adjlist[col1].link;
adjlist[col1].link = p1;
}
for(i=1;i<=n;i++)
{
p1 = (edgeNode*)malloc(sizeof(edgeNode));
p1->no = i;
p1->weight = 0;
p1->next = adjlist[0].link;
adjlist[0].link = p1;
}
lowcost[0] = 0;
}
//尋找v0到,每一個節點的最短路徑
bool Bellman_Ford(vexNode *adjlist,int *lowcost,int *parent,const int n)
{
int i,j;
for(j=0;j<n;j++)
{
for(i=0;i<=n;i++)
{
edgeNode *p1 = adjlist[i].link;
while(p1 != NULL)
{
if(lowcost[i]+p1->weight <lowcost[p1->no])
{
lowcost[p1->no] = lowcost[i]+p1->weight;
parent[p1->no] = i;
}
p1 = p1->next;
}
}
}
//檢查有無負回路
for(i=1;i<=n;i++)
{
edgeNode *p2 = adjlist[i].link;
while(p2 != NULL)
{
if(lowcost[p2->no]>lowcost[i]+p2->weight)
return false;
p2 = p2->next;
}
}
return true;
}
int _tmain(int argc, _TCHAR* argv[])
{
int cases;
cout<<"請輸入案例的個數:";
cin>>cases;
while(cases--)
{
int i,j;
int n,m;
cout<<"請輸入差分矩陣的行數(m)與列數(n):";
cin>>m>>n;
cout<<"請輸入差分矩陣:"<<endl;
for(i=1;i<=m;i++)
for(j=1;j<=n;j++)
cin>>a[i][j];
cout<<"請輸入約束集:"<<endl;
for(i=1;i<=m;i++)
cin>>w[i];
//創建鄰接表
createGraph(adjlist,parent,lowcost,w,m,n);
//輸出鄰接表
/*
for(i=0;i<=n;i++)
{
edgeNode *p = adjlist[i].link;
cout<<i<<":";
while(p != NULL)
{
cout<<"("<<p->no<<","<<p->weight<<") ";
p = p->next;
}
cout<<endl;
}
*/
//調用Bellman-Ford算法
bool flag = Bellman_Ford(adjlist,lowcost,parent,n);
if(!flag)
cout<<"無解"<<endl;
else
{
//輸出解集
cout<<"其中一個解集為(此解集加上一個任意的常數d也是其解集):"<<endl;
for(i=1;i<=n;i++)
cout<<"x"<<i<<"="<<lowcost[i]<<endl;
}
}
system("pause");
return 0;
}
---------------------------------------------------程序測試---------------------------------------------------

請輸入案例的個數:1
請輸入差分矩陣的行數(m)與列數(n):8 5
請輸入差分矩陣:
1 -1 0 0 0
1 0 0 0 -1
0 1 0 0 -1
-1 0 1 0 0
-1 0 0 1 0
0 0 -1 1 0
0 0 -1 0 1
0 0 0 -1 1
請輸入約束集:
0 -1 1 5 4 -1 -3 -3
其中一個解集為(此解集加上一個任意的常數d也是其解集):
x1=-5
x2=-3
x3=0
x4=-1
x5=-4
請按任意鍵繼續. .
作者 heyongluoyao8