問題:
給定兩個字符串s1和s2,要求判定s2是否能夠被s1做循環移位得到的字符串包含。
解法:
我們在對s1進行循環移位時,保留前面移走的數據,會發現只要將s1復制一份接在後面就能夠包含匹配的所有情況。然後只要在s1中查找s2的位置就可以了,我們使用KMP算法在時間O(m+n)內就能夠找出這個位置。
KMP算法還是一個比較難理解的算法之一,它的改進在於每當一趟匹配過程中出現字符比較不等時,不需回溯i指針,而是利用已經得到的“部分匹配”的結果將模式串向右“滑動”盡可能遠的一段距離後,繼續進行比較。
模式串T開頭的串被稱為前綴子串(下圖字符串1...f(k-1)-1表示一個前綴子串),在T中第k個字符左邊的子串被稱為位置k的左子串(下圖字符串k-f(k-1)...k-2表示與該前綴子串相匹配的位置k-1的左子串)。這裡我們用動態規劃的思路實現這個算法,在形式上與書上的實現方式相差比較大,但效率是一樣,並且會更好理解和記憶
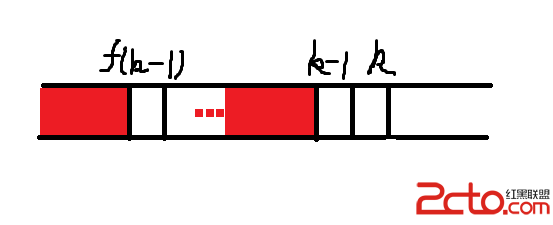
階段:在位置k的所有左子串中,所選出的與前綴子串相匹配的長度最長的左子串的後一個字符的位置為f[k],k=1,2...n,這個後一個字符的位置很特別,它表示若第k個字符匹配失敗,就將模式串向右滑動到第f[k]個字符,並與f[k]字符進行比較。
狀態:若第k個字符匹配失敗接下去只有一個待匹配的字符f[k]。
決策:決定第k字符匹配失敗之後下一個待匹配的字符有多種策略,它依次可能是f[k-1], f[f[k-1]], ... , f...f[k-1],且這個序列是遞減的,我們取第一個滿足T[k-1]==T[f...f[k-1]]的那個f...f[k-1],我們將其命為f*[k-1],f*[k-1]+1的位置就大概可被稱為第k個字符匹配失敗後接下去要匹配的字符。但若位置f*[k-1]+1的字符等於第k個字符,那我們知道第k個字符匹配失敗,第f*[k-1]+1個字符必然也匹配失敗,所以若不相等我們可以直接將第f*[k-1]+1個字符設為第k個字符的下一個待匹配字符,若相等我們將第f*[k-1]+1匹配失敗之後的那個字符f[f*[k-1]+1]作為第k個字符的下一個待匹配字符。
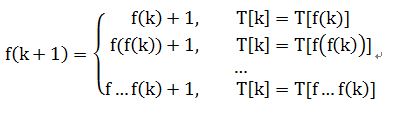
[cpp]
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
#define MAXN 10001
char S[MAXN];
char T[MAXN];
// 動態規劃的KMP算法
int nxt[MAXN];
void state_transfer(char *T, int n, int *next)
{
int k, u;
// next[k]表示k的左子串與前綴子串相匹配的字符數
next[1] = 0; // 若第一個字符都不匹配,則移位
for (k=2; k<=n; k++) // 階段k,只有一個狀態next[k]
{
// 決策u表示k-1的左子串與前綴子串相匹配的字符數
// 找到長度為u的前綴子串使得其最後一個字符等於第k-1字符
for (u=next[k-1]; u>=1; u=next[u])
if (T[k-1] == next[u]) break;
// 若第k字符等於所找到的前綴子串的下一個字符
// 則若第k字符匹配失敗,則第u+1字符肯定也失敗,
// 所以不必嘗試匹配第u+1字符,直接匹配next[u+1]字符
if (T[k] != T[u+1])
next[k] = u+1;
else
next[k] = next[u+1];
}
}
// 從目標串S中找出模式串T
int findTfromS(char *S, int n, char *T, int *next, int m)
{
int i, j;
i=j=1;
while (i<=n && j<=m)
{
// 若S的第i字符匹配T的第j字符,則接著匹配下一字符
// 否則進而比較T的第next[j]字符
if (j==0 || S[i]==T[j]) {i++; j++;}
else j = next[j];
}
return i-m;
}
int main()
{
S[0] = T[0] = '0';
scanf("%s", S+1);
strcpy(T, S);
strcpy(S+strlen(S), T+1);
scanf("%s", T+1);
state_transfer(T, strlen(T)-1, nxt);
int pos = findTfromS(S, strlen(S)-1, T, nxt, strlen(T)-1);
if (pos == strlen(S))
printf("false\n");
else
printf("true: %d\n",pos);
}
作者:linyunzju