背包問題:
給定n種物品(每種物品僅有一件)和一個背包。物品i的重量是wi ,其價值為pi ,背包的容量為w。問應如何選擇物品裝入背包,使得裝入背包中的物品的總價值最大?
l 如果在裝入背包時,物品可以切割,即可以只裝入一部分,這種情況下的問題稱為背包問題。
l 在裝入背包時,每種物品i只有兩種選擇,裝入或者不裝入,既不能裝入多次,也不能只裝入一部分。因此,此問題稱為0-1背包問題。
要想得到最優解,就要在效益增長和背包容量消耗兩者之間尋找平衡。也就是說,總應該把那些單位效益最高的物體先放入背包。
背包問題可看做是一種回溯:
每個包是一個節點, 節點共有2個候選值0、1 。 0代表不放人背包中, 1代表放入背包中。
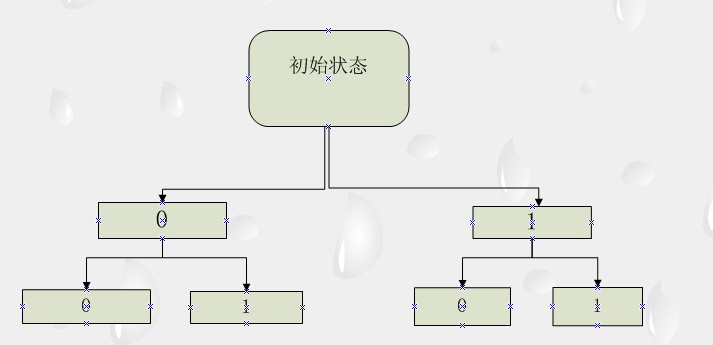
因此,背包問題就轉換為找到滿足條件的路徑問題。
因此,可用回溯方法解決。
回溯方法解決背包問題:
方法一:
// 判斷節點(I,j)是否為解路徑上的節點,其中:
//
// i表示解路徑上的第i個測試節點、j表示該節點的某個候選值
// A[i] 保存第i個節點選用的值
BOOL TestNode(I ,j)
{
更新相關參數值(假定選擇了此候選值j,因此更新受影響的參數值);
與0—(i-1) 層進行判斷,看是否與以遍歷的節點有沖突
若有沖突, 則返回FALSE;
若無沖突, 則 將節點i的值j,保存到對應的數組中A[I]=J;
判斷I是否為最後一層,
若是最後一層,則成功找到一條解路徑,返回TRUE;
若不是最後一層,則判斷第i+1層是否有正確的節點。
BOOL bFlag=FALSE;
FOR(k=0;k< CANDIDATA_NUM;k++) //候選值【0,。。。,CANDIDATA_NUM -1】
{
If(TestNode(i+1,k))
{
找到一個解;
bFlag=True;
}
//不管TestNode(i+1,k)是成功的還是失敗的,退出後,都要對參數進行還原
還原相關參數值(撤銷了候選值k,因此要還原受影響的參數值);
}
RETURN bFlag;
}
[cpp]
int m,n=5,x[10]={0};
int w[6]={0,2,2,6,5,5},v[6]={0,6,3,5,4,6};
int c=10;
int cw=0,cv=0,bestv=0;
BOOL TestNode(int i,int j){ // 第 i個物品的 候選值為0和1
//更新相關參數值
cw+=w[i]*j;
cv+=v[i]*j;
//與之前的物品相比 有無沖突
if (cw>c)
return FALSE;
//無沖突,添加至解路徑
x[i]=j;
// 到此為止 0--i行 均無沖突
// 如果是最後一行 成功找到一個解
if(i==n){
for(i=1;i<=n;i++)
printf("%d",x[i]);
if(cv>bestv)
bestv=cv;
printf("\n");
return TRUE;
}
//如果不是最後一行 則判斷i+1行
BOOL bSuit=FALSE;
for (int k=0;k<=1;k++)
{
//第i+1行存在合適位置
if (TestNode(i+1,k))
bSuit=TRUE;
//還原相關參數
cw-=w[i+1]*k;
cv-=v[i+1]*k;
}
return bSuit;
}
void Bag()
{
for (int i=0;i<=1;i++)
{
TestNode(1,i);
}
}
或 不更新與還原相關變量, 而是根據已知信息推導相關變量值
[cpp]
int m,n=5,x[10]={0};
int w[6]={0,2,2,6,5,5},v[6]={0,6,3,5,4,6};
int c=10;
int cw=0,cv=0,bestv=0;
BOOL TestNode(int i,int j){ // 第 i個物品的 候選值為0和1
//根據已知 推倒相關參數值
cw=0;
cv=0;
for (int k=1;k<=i-1;k++)
{
cw+=x[k]*w[k];
cv+=x[k]*v[k];
}
cw+=w[i]*j;
cv+=v[i]*j;
//與之前的物品相比 有無沖突
if (cw>c)
return FALSE;
//無沖突,添加至解路徑
x[i]=j;
// 到此為止 0--i行 均無沖突
// 如果是最後一行 成功找到一個解
if(i==n){
for(i=1;i<=n;i++)
printf("%d",x[i]);
if(cv>bestv)
bestv=cv;
printf("\n");
return TRUE;
}
//如果不是最後一行 則判斷i+1行
BOOL bSuit=FALSE;
for (int k=0;k<=1;k++)
{
//第i+1行存在合適位置
if (TestNode(i+1,k))
bSuit=TRUE;
}
return bSuit;
}
void Bag()
{
for (int i=0;i<=1;i++)
{
TestNode(1,i);
}
}
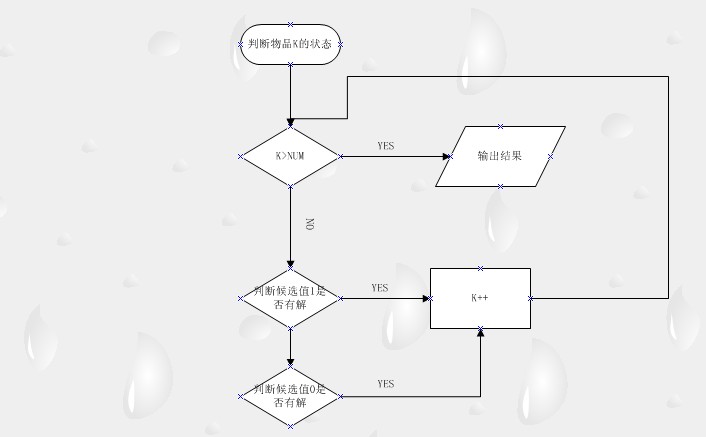
方法二:
根據背包問題的特殊性 ,可簡化算法
[cpp]
int m,n=5,x[10]={0};
int w[6]={0,2,2,6,5,5},v[6]={0,6,3,5,4,6};
int c=10;
int cw=0,cv=0,bestv=0;
int ok(int k)
{
int u=1;
if(cw>c)
u=0;
return u;
}
int f(int k)
{
int i;
if (k>n)
{
for(i=1;i<=n;i++)
printf("%d",x[i]);
if(cv>bestv)
bestv=cv;
printf("\n");
}
else
{
x[k]=1; //判斷候選值1
cw+=w[k];
cv+=v[k];
if(ok(k))
f(k+1);
cw-=w[k]; //判斷候選值0
cv-=v[k];
x[k]=0;
if(ok(k))
f(k+1);
}
return k;
}
作者:shuilan0066