[cpp] view plaincopyprint?/*
有源匯 有上下界 求可行流
有源匯可以轉化為無源匯:添加一條邊t~s (0,0x7fffffff) 就成了無源匯
基本流程是:
構造附加網絡(添加新源 新匯 分離必要弧)
求附加網絡的最大流
若新源 新匯 相鄰的邊都是滿流,則存在可行流
題意:
有個表格,給出每行的和以及每列的和 還有某些元素的要求
求一個符合條件的表格
添加新的源匯後,分離必要弧(必有一端是新源或新匯,必須滿流才有可行流)
這時候有兩種(新源ss新匯tt):
1.添加 (u,v)流量為上下界之差 (ss,v) 和 (u,tt) 的流量都是 下界流量
可以這樣理解:(u,v)流量為上下界之差 是因為要改造成下界流量為0的
(ss,v)流量是下界流量 是因為要補充(u,v)中的下界流量,使其直接到v
(u,tt)流量是下界流量 從u之前流過來的流量中,無法通過全部(u,v),其下界部分通過這條邊直接到tt
上面那篇文站就是這樣講的,但是他寫的時候用的是第二種
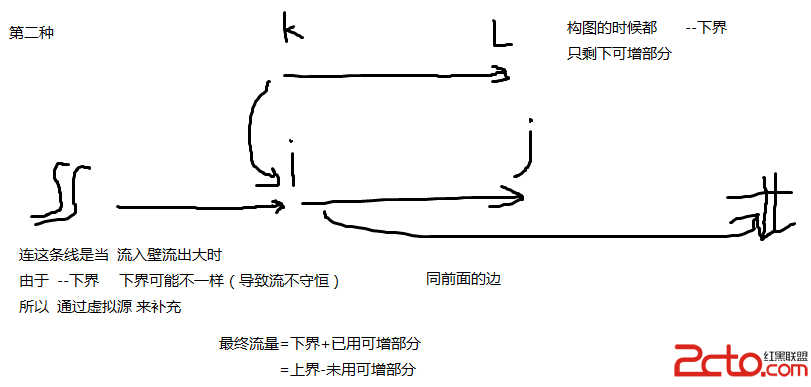
2.添加 (u,v)流量為上下界之差 (ss,u) 和 (u,tt) 的流量都是 流入u的所有下界流量之和 減去 流出u的所有下界流量之和(有圖)
這兩種方法分別是從 邊 點 兩個方面進行的
把邊或點的下界分離出來,使所有的邊或點的下界都為0,轉化為普通的最大流問題
下界部分直接由ss提供或直接流向tt
*/
#include<iostream>
#include<string>
using namespace std;
#define N 235
int map[N][N],m,n,s,t,x,y,up[N][N],low[N][N],yu[N],num[N],d[N];
int min(int a,int b){return a<b?a:b;}
int max(int a,int b){return a>b?a:b;}
void ini()
{
memset(low,0,sizeof(low));
memset(map,0,sizeof(map));
memset(yu,0,sizeof(yu));
for(int i=0;i<=m;++i)
for(int j=0;j<=n;++j)
up[i][j]=0x7fffffff;
}
int build()
{
for(int i=1;i<=m;i++)
for(int j=1;j<=n;j++)
if(low[i][j]>up[i][j]) return 0;
else{
yu[i]-=low[i][j],yu[j+m]+=low[i][j];//這裡的m寫成了n
map[i][j+m]=up[i][j]-low[i][j];
}
return 1;
}
int sap(int u,int f)
{
if(u==y)//到達終點
return f;
int v,mind=y,last=f,cost;//mind=點數-1 若從0開始,即為最後那個點
for(v=0;v<=y;++v)
{
if(map[u][v]>0)
{
if(d[u]==d[v]+1)
{
cost=sap(v,min(last,map[u][v]));
map[u][v]-=cost;
map[v][u]+=cost;
last-=cost;
if(d[x]>=y+1)
return f-last;
if(last==0)
break;
}
if(d[v]<mind)
mind=d[v];
}
}
if(last==f)
{
--num[d[u]];
if(num[d[u]]==0)
d[x]=y+1;
d[u]=mind+1;
++num[d[u]];
}
return f-last;
}
void limitflow()//
{
int i,j,c=0;//c最大流的流量
x=t+1,y=t+2;//新源 新匯
for(i=s;i<=t;++i)
if(yu[i]>0) map[x][i]=yu[i];//必要弧
else if(yu[i]<0) map[i][y]=-yu[i];//必要弧
map[t][s]=0x7fffffff;//把原圖改成無源匯
memset(d,0,sizeof(d));
memset(num,0,sizeof(num));
for(num[x]=y+1;d[x]<y+1;)//y+1點數
c+=sap(x,0x7fffffff);//用sap求最大流
for(i=s;i<=t;++i)//判斷是否滿流
if(map[x][i])
{
cout<<"IMPOSSIBLE"<<endl<<endl;
return;
}
for(i=1;i<=m;++i)//輸出可行流
{
for(j=1;j<n;++j)
cout<<(up[i][j]-map[i][j+m])<<" ";//上界-未用可增部分
cout<<(up[i][n]-map[i][n+m])<<endl;
}
cout<<endl;
}
int main()
{
int cas,sum1,sum2,i,j,a,b,num,c,f1,f2,t1,t2;
string op;
cin>>cas;
while(cas--)
{
cin>>m>>n;
s=0,t=m+n+1,sum1=sum2=0;
ini();
for(i=1;i<=m;++i) cin>>a,yu[s]-=a,yu[i]+=a,sum1+=a;
for(;i<=m+n;++i) cin>>a,yu[i]-=a,yu[t]+=a,sum2+=a;
cin>>c;
while(c--)//他的處理方法很好
{
cin>>a>>b>>op>>num;
f1=t1=a;
f2=t2=b;
if(a==0)
f1=1,t1=m;
if(b==0)
f2=1,t2=n;
for(i=f1;i<=t1;++i)
for(j=f2;j<=t2;++j)
if(op[0]=='=')
low[i][j]=max(num,low[i][j]),up[i][j]=min(num,up[i][j]);
else if(op[0]=='>')
low[i][j]=max(num+1,low[i][j]);
else if(op[0]=='<')
up[i][j]=min(num-1,up[i][j]);
}
if(sum1==sum2&&build()) limitflow();
else cout<<"IMPOSSIBLE"<<endl<<endl;
}
return 0;
}
/*
有源匯 有上下界 求可行流
有源匯可以轉化為無源匯:添加一條邊t~s (0,0x7fffffff) 就成了無源匯
基本流程是:
構造附加網絡(添加新源 新匯 分離必要弧)
求附加網絡的最大流
若新源 新匯 相鄰的邊都是滿流,則存在可行流
題意:
有個表格,給出每行的和以及每列的和 還有某些元素的要求
求一個符合條件的表格
一個比較詳細的講解 http://blog.csdn.net/water_glass/article/details/6823741
添加新的源匯後,分離必要弧(必有一端是新源或新匯,必須滿流才有可行流)
這時候有兩種(新源ss新匯tt):
1.添加 (u,v)流量為上下界之差 (ss,v) 和 (u,tt) 的流量都是 下界流量
可以這樣理解:(u,v)流量為上下界之差 是因為要改造成下界流量為0的
(ss,v)流量是下界流量 是因為要補充(u,v)中的下界流量,使其直接到v
(u,tt)流量是下界流量 從u之前流過來的流量中,無法通過全部(u,v),其下界部分通過這條邊直接到tt
上面那篇文站就是這樣講的,但是他寫的時候用的是第二種
2.添加 (u,v)流量為上下界之差 (ss,u) 和 (u,tt) 的流量都是 流入u的所有下界流量之和 減去 流出u的所有下界流量之和(有圖)
這兩種方法分別是從 邊 點 兩個方面進行的
把邊或點的下界分離出來,使所有的邊或點的下界都為0,轉化為普通的最大流問題
下界部分直接由ss提供或直接流向tt
*/
#include<iostream>
#include<string>
using namespace std;
#define N 235
int map[N][N],m,n,s,t,x,y,up[N][N],low[N][N],yu[N],num[N],d[N];
int min(int a,int b){return a<b?a:b;}
int max(int a,int b){return a>b?a:b;}
void ini()
{
memset(low,0,sizeof(low));
memset(map,0,sizeof(map));
memset(yu,0,sizeof(yu));
for(int i=0;i<=m;++i)
for(int j=0;j<=n;++j)
up[i][j]=0x7fffffff;
}
int build()
{
for(int i=1;i<=m;i++)
for(int j=1;j<=n;j++)
if(low[i][j]>up[i][j]) return 0;
else{
yu[i]-=low[i][j],yu[j+m]+=low[i][j];//這裡的m寫成了n
map[i][j+m]=up[i][j]-low[i][j];
}
return 1;
}
int sap(int u,int f)
{
if(u==y)//到達終點
return f;
int v,mind=y,last=f,cost;//mind=點數-1 若從0開始,即為最後那個點
for(v=0;v<=y;++v)
{
if(map[u][v]>0)
{
if(d[u]==d[v]+1)
{
cost=sap(v,min(last,map[u][v]));
map[u][v]-=cost;
map[v][u]+=cost;
last-=cost;
if(d[x]>=y+1)
return f-last;
if(last==0)
break;
}
if(d[v]<mind)
mind=d[v];
}
}
if(last==f)
{
--num[d[u]];
if(num[d[u]]==0)
d[x]=y+1;
d[u]=mind+1;
++num[d[u]];
}
return f-last;
}
void limitflow()//
{
int i,j,c=0;//c最大流的流量
x=t+1,y=t+2;//新源 新匯
for(i=s;i<=t;++i)
if(yu[i]>0) map[x][i]=yu[i];//必要弧
else if(yu[i]<0) map[i][y]=-yu[i];//必要弧
map[t][s]=0x7fffffff;//把原圖改成無源匯
memset(d,0,sizeof(d));
memset(num,0,sizeof(num));
for(num[x]=y+1;d[x]<y+1;)//y+1點數
c+=sap(x,0x7fffffff);//用sap求最大流
for(i=s;i<=t;++i)//判斷是否滿流
if(map[x][i])
{
cout<<"IMPOSSIBLE"<<endl<<endl;
return;
}
for(i=1;i<=m;++i)//輸出可行流
{
for(j=1;j<n;++j)
cout<<(up[i][j]-map[i][j+m])<<" ";//上界-未用可增部分
cout<<(up[i][n]-map[i][n+m])<<endl;
}
cout<<endl;
}
int main()
{
int cas,sum1,sum2,i,j,a,b,num,c,f1,f2,t1,t2;
string op;
cin>>cas;
while(cas--)
{
cin>>m>>n;
s=0,t=m+n+1,sum1=sum2=0;
ini();
for(i=1;i<=m;++i) cin>>a,yu[s]-=a,yu[i]+=a,sum1+=a;
for(;i<=m+n;++i) cin>>a,yu[i]-=a,yu[t]+=a,sum2+=a;
cin>>c;
while(c--)//他的處理方法很好
{
cin>>a>>b>>op>>num;
f1=t1=a;
f2=t2=b;
if(a==0)
f1=1,t1=m;
if(b==0)
f2=1,t2=n;
for(i=f1;i<=t1;++i)
for(j=f2;j<=t2;++j)
if(op[0]=='=')
low[i][j]=max(num,low[i][j]),up[i][j]=min(num,up[i][j]);
else if(op[0]=='>')
low[i][j]=max(num+1,low[i][j]);
else if(op[0]=='<')
up[i][j]=min(num-1,up[i][j]);
}
if(sum1==sum2&&build()) limitflow();
else cout<<"IMPOSSIBLE"<<endl<<endl;
}
return 0;
}
作者:qq172108805