下面是復制別人的解析後根據我不懂的地方自己補充修改的:
二部圖(也叫二分圖)概念:
1.何為二部圖
如果V(G)可以分到兩個集合X,Y中,且X和Y內部沒有G的邊.那麼圖G就是一個二部圖(等價於圖G是可二頂點著色的)下圖便是一個二部圖.
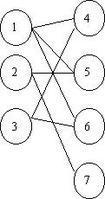
2.二部圖的性質
一個圖是二部圖當且僅當圖G中沒有奇環.比如說一個三角形就不可能分成兩個部分,並且每個部分內部沒有邊,但一個正方形就可以.
3.如何得到二部圖的每個部分
任意選一個頂點,所有到該點距離為偶數的點構成的集合便是G中的一部分,距離為奇數的點為另一部分
4.何為匹配
圖G的一個匹配是一組沒有公共端點的邊構成的集合,如(圖一)兩條黑色的邊(1,4、2,5)構成一個大小為2的匹配,三條紅色的邊(1,4、2,5、3,6)構成一個大小為3的匹配.圖中的最大匹配數就是3。
該題就是求解一個二分圖的最大匹配,判定一個匹配是不是最大匹配就是通過尋找增廣路徑。如何尋找呢?
假設該題中女生為X部,男生為Y部,定義幾個變量,G[u][i]代表u,i兩點之間的連接情況,marry[i] =u表示Y部中的第i個男生與女生u配對,visit[i] 表示Y部中第i個男生有沒有女生找過,兩個數組初始化為0。
在每次尋找增廣路徑時,我們都將visit[i]重置,因為每次尋找增廣路徑就是讓他們每個男生都有重新選擇的機會,然後判定這種新的匹配方式能否產生更多的匹配。
step1:從一個女生開始,掃描所有在另外一個部分(Y部)與之相連的點,沒有邊或者已經給過機會的男生(他們或許已經找到新另一半,或者他不願與前女伴分手)的不予考慮。
for (int i = 1; i <= N; ++i) {
if (!G[u][i] || visit[i])
continue;
......
}
step2:兩兩之間有邊,並且第i個男生在這一輪新的配對中暫時沒有被女生找到的話(就是step1的if判定失敗),那麼這個男生就算被女生找過了。
visit[i] = 1;
step3:現在我們這樣來辦,如果第i個男生之前沒有女生配對的話,那麼馬上將他們聯系起來,因為這必將是新的一對,並且返回1,表示尋找到了增廣路徑。還有一種情況,那就
該男生之前有女生配對,那麼我們就策劃讓其以前配對的女生另外找一個男生,這不難實現,再次調用這個函數即可。
if (!marry[i] || path(marry[i])) {
marry[i] = u;
return 1;
}
step4:如果所有的男生由於各種原因都不願與該女生配對的話,返回0,表示尋找增廣路徑失敗。
我們調從外部調用這個函數N次(N代表女生的個數),表示每次抱著給這個女生找有好男友的決心,雖然過程中可能會拆散其他對,但我能保證只有當新配對的人數多余上次匹配結果我才這樣去做。
注意:1.假設是第k次從外部調用該函數的話,執行該函數的過程中一定不會牽涉到第k+1到N號女生的匹配情況,因為我們每次頂多是拆散以前的配對過的女生去完成新匹配。
2.為什麼能保證配對的對數增加呢?如果函數執行成功,我們為第k號女生完成了匹配,並且為所有為之被拆散的女生找到了新的對象,所以匹配數會增加1。
一個匹配M是圖G的最大匹配當且僅當圖G中不存在M-增廣路徑. M-增廣路徑是一條邊交替出現在匹配M和不出現在匹配M中的路徑,且兩個端點沒有被M中的邊覆蓋。若是一個圖有M-增廣路徑,就得到了一個更大的匹配。所謂交替出現在M和不出現在M中的路徑就是撮合一對,拆散一對的過程。
代碼如下:
[cpp]
#include<iostream>
#include<stdio.h>
#include<math.h>
#include<string.h>
#include<stdlib.h>
#include<algorithm>
using namespace std;
int map[505][505],vb[505],marryb_g[505];
int k,n,m;
int getpath(int u)
{
int i;
for(i=1;i<=m;i++)
{
if(!map[u][i] || vb[i])
continue;
vb[i]=1;
if(!marryb_g[i] || getpath(marryb_g[i]))
{
marryb_g[i]=u;
return 1;
}
}
return 0;
}
int main()
{
int i,a,b;
while(scanf("%d",&k)!=EOF && k)
{
memset(map,0,sizeof(map));
memset(marryb_g,0,sizeof(marryb_g));
scanf("%d%d",&n,&m);
for(i=0;i<k;i++)
{
scanf("%d%d",&a,&b);
map[a][b]=1;
}
int ans=0;
for(i=1;i<=n;i++)
{
memset(vb,0,sizeof(vb));
if(getpath(i))
ans++;
}
printf("%d\n",ans);
}
return 0;
}