編程之美的課後題也有一個和整個題目一樣的。(P269)
題目
這個題目的題意很容易理解,在一個N*M的格子裡,我們現在有兩種類型的 磚塊,1 * 2 和 2 * 1,問一共有多少種方案,可以將整個N*M的空間都填滿。
最簡單的例子就是下面的了:

編程之美中題目:
某年夏天,位於希格瑪大廈四層的微軟亞洲研究院對辦公樓的天井進行了一次大 規模的裝修.原來的地板鋪有 N×M 塊正方形瓷磚,這些瓷磚都已經破損老化了,需要予以 更新.裝修工人們在前往商店選購新的瓷磚時,發現商店目前只供應長方形的瓷磚,現在的 一塊長方形瓷磚相當於原來的兩塊正方形瓷磚, 工人們拿不定主意該買多少了, 讀者朋友們 請幫忙分析一下:能否用 1×2 的瓷磚去覆蓋 N×M 的地板呢?
我們在這裡指分析第一個陳述,其實第二個陳述是一樣的思路:
這個題目類屬於狀態壓縮DP,對於狀態壓縮DP,其實最簡單的理解就是把狀態用比特位的形式表示出來,我們會在下面用例子來說明。
假如現在我們在鋪磚 位置(i, j), 並且假設之前的位置已經鋪設好的了,在這個位置,我們的選擇:
1. 不用鋪磚了,可能在(i-1, j)的時刻已經被豎著鋪上了,然後考慮的是(i, j+1)
2. 橫鋪磚,將(i, j+1)也鋪上了,然後考慮的是(i, j+2)
3. 豎著鋪磚,(將i,j)和(i+1,j)鋪上一個豎立的轉頭。
所以我們如下翻譯我們的選擇,在位置(i, j) 如果我們選擇橫著貼磚,那麼將(i, j), (i, j+1)都填寫成1, 如果豎著貼磚,我們將(i,j)填寫成0, 將(i+1, j)填寫成1.
為什麼要這麼計數呢,我覺得應該這樣理解:
1. 在橫著貼磚的時候,(i, j), (i, j+1) 都是1,這個值其實對下一行如何選擇沒有影響。
2. 豎著貼磚的第二個,我們也選擇了1, 因為這個磚頭結束了,對下一行如何選擇依然沒有影響。
3. 而豎著的第一個磚頭,這個磚頭是對下面有影響的,如果(i,j)是0,那麼(i+1, j)只有是1的情況下才能滿足條件。
(這涉及到接下來的 狀態兼容性問題)
對於豎著貼磚為什麼這樣選擇,這樣選擇的一個好處是,我們在處理最後一行的時候,可以保證最後一行都是1, 因為最後一行絕對不能成為 豎磚開始,所以很容易取得最後的解。
好了,我們把這樣理解的方案畫成圖:
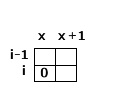
如果我們將每一行都理解成一個二進制數字,那麼
Row1 = 51, Row2 = 15, Row3 = 48, Row4 = 63, Row5 = 51, Row6 = 63.
最後轉頭鋪滿的狀態,一定是最後一行全是1。
我們用DP(i,j) 表示如下含義: 當第i行,達到狀態j的時候,所能采取的方案數目。 所以明顯我們的最後目的是求 DP(N, 2^(M-1)-1);
我們再來簡單的分析一下為什麼問題可以滿足動態規劃, 加入現在分析的對象是 DP(i,j), 那麼這一行有多少種鋪設辦法是和上一行相關的,
如果上一行的某個狀態DP(i-1,k) 可以達到 DP(i, j) 我們認為這兩個狀態是兼容的,如果DP(i-1,k)和DP(i, j)兼容並且 DP(i-1, k)有S中鋪設方案,那麼DP(i, j)就可以從DP(i-1, k)
這條路徑中獲得S個方案。 當然這裡k的取值可以是 0 ~~~~ 2^(M-1) -1種取值。
現在我們來理解一下,什麼叫做 j, k 兼容。
其實我們在上面已經基本給出分析, 如果我們現在鋪設 (i,x) x這裡表示第i行,第x列
1. 如果值 i 行,j 在x位上的值是0, 那麼第 i-1行,j的值在x位上一定是1。因為不可能在同一列相鄰的位置鋪兩個豎著的 第一個,如果滿足下一步測試的是(i, x+1), 否則直接返回不兼容。
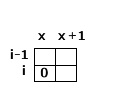
2. 如果值 i 行,j在x位置的值是1 .
{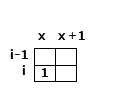
那麼有可能有兩種情況:
1. (i-1, x)是0, 這個時候一定是豎著鋪設了,下一步檢測的是(i, x + 1)
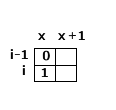
2. (i-1, x) 是1, 如果是這樣的話,那麼(i, x)一定是要選擇橫著鋪了,那麼(i,x+1)也一定是1,並且(i-1, x + 1)一定是1(如果是0,就是豎著鋪了),如果不滿足就返回不兼容,滿足條件 就測試(i, x + 2)
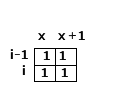
}
對於第一行的兼容性,我們要做一下特別的分析,在第一行中,要麼放0, 要麼放1。
加入當前測試的是 DP(0, j)的第 x的比特位,即第0行,x列
1. 如果x是1,那麼 x + 1 也一定是1,然後測試到 x + 2
2. 如果x是0, 那麼直接測試下一個 x + 1
補充說明一點,當測試循環中,我們有時候必須要移動 1 位,有時候移動2位,當需要移動2位並且 x == M - 1(M列數)的時候,說明已經不可能兼容了。
根據上面的分析就不難寫出代碼了:
[cpp]
#include <stdio.h>
#include <memory.h>
#include <math.h>
#include <algorithm>
using namespace std;
#define MAX_ROW 11
#define MAX_STATUS 2048
long long DP[MAX_ROW][MAX_STATUS];
int g_Width, g_Height;
bool TestFirstLine(int nStatus) //test the first line
{
int i = 0;
while( i < g_Width)
{
if(nStatus & (0x1 << i))
{
if( i == g_Width -1 || (nStatus & (0x1 << (i+1))) == 0)
{
return false;
}
i += 2;
}
else
{
i++;
}
}
return true;
}
bool CompatablityTest(int nStatusA, int nStatusB) // test if status (i, nStatusA) and (i-1, nStatusB) is compatable.
{
int i = 0;
while( i < g_Width)
{
if( (nStatusA & (0x1 << i)) == 0)
{
if((nStatusB & (0x1 << i)) == 0)
{
return false;
}
i++;
}
else
{
if((nStatusB & (0x1 << i)) == 0 )
{
i++;
}
else if( (i == g_Width - 1) || ! ( (nStatusA & (0x1 << (i+1))) && (nStatusB & (0x1 << (i + 1)))) )
{
return false;
}
else
{
i += 2;
}
}
}
return true;
}
int main()
{
int i,j;
int k;
while(scanf("%d%d", &g_Height, &g_Width) != EOF )
{
if(g_Width == 0 && g_Height == 0)
{
break;
}
if(g_Width > g_Height)
{
swap(g_Width, g_Height);
}
int nAllStatus = 2 << (g_Width-1);
memset(DP, 0, sizeof(DP));
for( j = 0; j < nAllStatus; j++)
{
if(TestFirstLine(j))
{
DP[0][j] = 1;
}
}
for( i = 1; i < g_Height; i++)
{
for( j = 0; j < nAllStatus; j++)// iterate all status for line i
{
for( k = 0; k < nAllStatus; k++) // iterate all status for line i-1
{
if(CompatablityTest(j, k))
{
DP[i][j] += DP[i-1][k];
}
}
}
}
printf("%lld\n", DP[g_Height-1][nAllStatus - 1]);
}
return 0;
}
幾點注意:因為算法 復雜度是 H * (W^4) 所以當 W > H的時候,我們交換他們這樣適當降低復雜度。
另外數據到後面比較大,所以使用 long long( __int64)
作者:hopeztm