以前寫過一個證明,直接貼過來吧
主要是利用了反證法:
假設 s-t這條路徑為樹的直徑,或者稱為樹上的最長路
現有結論,從任意一點u出發搜到的最遠的點一定是s、t中的一點,然後在從這個最遠點開始搜,就可以搜到另一個最長路的端點,即用兩遍廣搜就可以找出樹的最長路
證明:
1 設u為s-t路徑上的一點,結論顯然成立,否則設搜到的最遠點為T則
dis(u,T) >dis(u,s) 且 dis(u,T)>dis(u,t) 則最長路不是s-t了,與假設矛盾
2 設u不為s-t路徑上的點
首先明確,假如u走到了s-t路徑上的一點,那麼接下來的路徑肯定都在s-t上了,而且終點為s或t,在1中已經證明過了
所以現在又有兩種情況了:
1:u走到了s-t路徑上的某點,假設為X,最後肯定走到某個端點,假設是t ,則路徑總長度為dis(u,X)+dis(X,t)
2:u走到最遠點的路徑u-T與s-t無交點,則dis(u-T) >dis(u,X)+dis(X,t);顯然,如果這個式子成立,
則dis(u,T)+dis(s,X)+dis(u,X)>dis(s,X)+dis(X,t)=dis(s,t)最長路不是s-t矛盾
附上一張第二種情況的圖
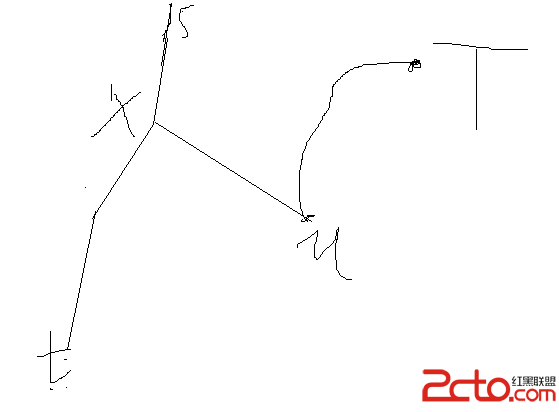
這道題讓你求出距離每個點最遠的點之間距離是多少,因為每個點走的最長路的重點肯定是直徑上的某個端點,所以,寫個bfs不斷的搜吧
[cpp]
#include<cstdio>
#include<cstring>
#include<vector>
#include<queue>
#include<algorithm>
using namespace std;
const int maxn = 30010;
vector<pair<int,int> > edge[maxn];
int dis1[maxn],dis2[maxn];
int n;
bool vis[maxn];
void bfs(int s,int &t,int dis[]){
fill(vis,vis+n,false);
queue<int> Q;
Q.push(s);vis[s]=true;
dis[s]=0;
int Max=0;
while(!Q.empty()){
int fr=Q.front();Q.pop();
int sz=edge[fr].size();
for(int i=0;i<sz;i++){
int v=edge[fr][i].first,w=edge[fr][i].second;
if(vis[v]) continue;
dis[v]=dis[fr]+w;
if(dis[v]>Max) t=v,Max=dis[v];
vis[v]=true;
Q.push(v);
}
}
}
int main()
{
int t,ca=1,a,b,w;
scanf("%d",&t);
while(t--)
{
scanf("%d",&n);
for(int i=0;i<n;i++) edge[i].clear();
for(int i=0;i<n-1;i++)
{
scanf("%d%d%d",&a,&b,&w);
edge[a].push_back(make_pair(b,w));
edge[b].push_back(make_pair(a,w));
}
int u,v,x;
bfs(0,u,dis1);
bfs(u,v,dis1);
bfs(v,x,dis2);
printf("Case %d:\n",ca++);
for(int i=0;i<n;i++)
{
printf("%d\n",max(dis1[i],dis2[i]));
}
}
return 0;
}
作者:haha593572013