感謝Dshawn的指導~~~~~~~
A. Tiling with Hexagons
給出a,b,c,根據圖中的形狀判斷有多少塊。
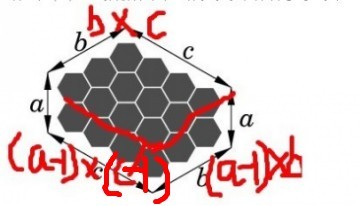
分為三個部分,總和就是b*c+(a-1)*(b+c-1)
也可以是不斷向內一層層的分解。
最外層為2*(b+c+a)-6。
而裡面一層為a-1,b-1,c-1,但是注意如果出現邊為1的話,就不能這麼統計了
不過邊為1剛好就是一個矩形
[cpp]
while(a>1&&b>1&&c>1){
ans+=2*(a+b+c)-6;
a--;b--;c-;;
}
ans+=a*b*c;
B. Forming Teams
有N個人,組成兩隊比賽,每一隊中不能有敵對狀態。
由於每個人最多有兩個敵對的,所以要麼是單鏈,要麼是簡單的環,要麼就是孤立狀態。
孤立狀態肯定不用考慮,隨便往哪隊放都可以
對於單鏈也不需要考慮,因為總是可以完整的分為兩隊
對於環先考慮偶數環,兩兩交錯,也是可以分為兩隊
但是奇數環就不可以了,總有一個人首尾相接,不能去任何一隊
所以結果就是如果有奇數環,總數減1,最後還需要判斷奇偶性
C. Hiring Staff
開始是固定的,K為幾,那麼就得有K個人從第一天開始,然後前n天都不用考慮,不過得有一個人去交接鑰匙,貪心處理,總是盡可能靠後,那就是第n天,從第n+1天只有一個人上班,如果k>1的話,就需要安排k--1個人從n+1天開始,如果k為1,那麼就是從2*n-1去交接鑰匙。總之每一個人都盡可能靠後,貪心模擬一下,直到第n+m+1天第一批人回來上班。
[cpp]
#include<iostream>
#include<cstring>
#include<queue>
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<vector>
#define N 1000000000
#define inf 1<<29
#define MOD 9973
#define LL long long
#define eps 1e-7
using namespace std;
int n,m,k;
vector<int>v;
int main(){
while(scanf("%d%d%d",&n,&m,&k)!=EOF){
v.clear();
for(int i=0;i<k;i++)
v.push_back(1);
v.push_back(n);
for(int i=1;i<k;i++)
v.push_back(n+1);
int l=2*n;
if(k==1)
l--;
while(l<n+m+1){
v.push_back(l);
if(l+1==n+m+1) break;
for(int i=1;i<k;i++)
v.push_back(l+1);
l+=n;
if(k==1) l--;
}
printf("%d\n%d",v.size(),v[0]);
for(int i=1;i<v.size();i++)
printf(" %d",v[i]);
puts("");
}
return 0;
}
D. Spider's Web
直接對於每一個區域,每一個小扇形進行枚舉,二分找到對於兩邊的數目,比較
感覺這樣不是很慢嗎,哎。。。。。n*k,1000*100000*log(100000
[cpp]
#include<iostream>
#include<cstring>
#include<queue>
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<vector>
#define N 1000000000
#define inf 1<<29
#define MOD 9973
#define LL long long
#define eps 1e-7
#define pb(a) push_back(a)
#define ub(v,a) upper_bound(v.begin(),v.end(),a)
using namespace std;
int main(){vector <int> v[1001];
int n,k,r;
while(scanf("%d",&n)!=EOF){
for(int i=1;i<=n;i++){
v[i].clear();
scanf("%d",&k);
while(k--){
scanf("%d",&r);
v[i].pb(r);
}
sort(v[i].begin(),v[i].end());
}
int ans=0;
for(int i=1;i<=n;i++){
int pre=i-1; pre=pre==0?n:pre;
int next=i+1; next=next==n+1?1:next;
for(int j=1;j<v[i].size();j++){
int x=ub(v[pre],v[i][j])-ub(v[pre],v[i][j-1]);
int y=ub(v[next],v[i][j])-ub(v[next],v[i][j-1]);
if(x!=y) ans++;
}
}
printf("%d\n",ans);
}
return 0;
}
E. Martian Luck
有個重要的結論:在k進制下個位數字之和相當於那個數字轉化成十進制以後mod(k-1),0的話就是k-1
那麼就能直接處理了,取前i項和的模數。用map記錄,然後遍歷一遍,就可以了。
不過由於k-1,0都最終記為0,所以這裡要處理一下,如果b既不是0,也不是k-1的話,那就無所謂了。
我們通過原數據,找一下所有0的數目,因為這個比較方便,
那麼如果b就是0,那麼就是我們最後統計的數目
如果b為k-1那麼我們要把原來統計的去掉b為0的情況。
[cpp]
#include<iostream>
#include<cstring>
#include<queue>
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<vector>
#include<map>
#define N 1000000000
#define inf 1<<29
#define MOD 9973
#define LL long long
#define eps 1e-7
#define pb(a) push_back(a)
#define ub(v,a) upper_bound(v.begin(),v.end(),a)
using namespace std;
int sum[100005],a[100005];
int main(){ www.2cto.com
int k,b,n;
while(scanf("%d%d%d",&k,&b,&n)!=EOF){
int m=k-1,pre=0;
for(int i=0;i<n;i++){
scanf("%d",&a[i]);
pre=(pre+a[i])%m;
sum[i]=pre;
}
map<int,int>mmap;
mmap.clear();
LL ans=0;
mmap[0]++;
for(int i=0;i<n;i++){
int t=(m+sum[i]-b)%m;
if(mmap.count(t))
ans+=mmap[t];
mmap[sum[i]]++;
}
LL ret=0;
for(int i=0;i<n;i++){
if(a[i]==0){
int j=1;
while(i+j<n&&a[j+i]==0) j++;
ret+=(LL)j*(j+1)/2;
i+=j;
}
}
if(b==0) ans=ret;
else if(b==k-1) ans-=ret;
printf("%I64d\n",ans);
}
return 0;
}