UVa 10382 - Watering Grass

原題：
n sprinklers are installed in a horizontal strip of grass l meters long and w meters wide. Each sprinkler is installed at the horizontal center line of the strip. For each sprinkler we are given its position as the distance from the left end of the center line and its radius of operation.
What is the minimum number of sprinklers to turn on in order to water the entire strip of grass?

Input
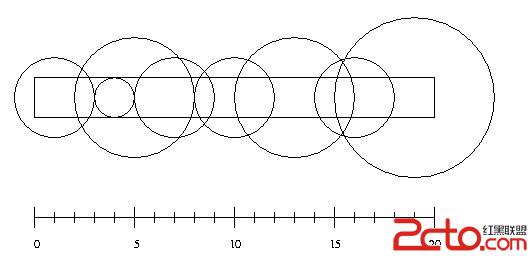
Input consists of a number of cases. The first line for each case contains integer numbers n, l and w with n <= 10000. The next n lines contain two integers giving the position of a sprinkler and its radius of operation. (The picture above illustrates the first case from the sample input.)
 
Output
For each test case output the minimum number of sprinklers needed to water the entire strip of grass. If it is impossible to water the entire strip output -1.
Sample input
8 20 2
5 3
4 1
1 2
7 2
10 2
13 3
16 2
19 4
3 10 1
3 5
9 3
6 1
3 10 1
5 3
1 1
9 1

Sample output
6
2
-1

題目大意：
有一塊草坪，長為l，寬為w，在它的水平中心線上有n個位置可以安裝噴水裝置，各個位置上的噴水裝置的覆蓋范圍為以它們自己的半徑ri為圓。求出最少需要的噴水裝置個數。

分析與總結：
這題的關鍵在於轉化

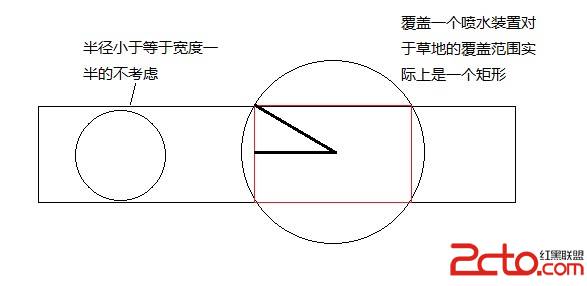
根據這圖可以看出，一個噴水裝置的有效覆蓋范圍就是圓中間的那個矩形。所以，在輸入的同時，進行預處理，轉換成矩形左邊的坐標和右邊的坐標。 這樣，其實就轉換成了經典的區間覆蓋問題。

代碼：
[cpp] 
/*
 * UVa: 10382 - Watering Grass
 * 貪心：最小覆蓋
 * Result: Accept
 * Time: 0.016s
 * Author: D_Double
 */ 
#include<iostream> 
#include<cmath> 
#include<cstdio> 
#include<algorithm> 
#define MAXN 10005 
using namespace std; 
int n,nIndex; 
double l, w; 
 
 
struct Node{ 
    double left; 
    double right; 
    friend bool operator < (const Node&a,const Node&b){ 
        return a.left < b.left; 
    } 
}arr[MAXN]; 
 
int main(){ 
    double p,r; 
    while(scanf("%d%lf%lf",&n,&l,&w)!=EOF){ 
        nIndex=0; 
        for(int i=0; i<n; ++i){ 
            scanf("%lf%lf",&p,&r); 
            if(w/2>=r)  
                continue; //直徑小於寬度的不考慮 
            double t=sqrt(r*r-w*w/4.0);  
            arr[nIndex].left=p-t; 
            arr[nIndex].right=p+t; 
            ++nIndex; 
        } 
 
        sort(arr,arr+nIndex); 
        int cnt=0; 
        double left=0, right=0; 
        bool flag=false; 
 
        if(arr[0].left <= 0 ){ 
            int i=0; 
 
            while(i < nIndex){ 
 
                int j=i; 
                while(j<nIndex && left>=arr[j].left){ 
                    if(arr[j].right > right) 
                        right=arr[j].right; 
                    ++j; 
                } 
                if(j==i) break;  // 如果上面的循環體沒有執行，說明之後都沒有滿足的了 
 
                ++cnt; 
                left=right; 
                i=j; 
 
                if(left>=l){ 
                    flag=true; 
                    break; 
                } 
            } 
        } 
        if(flag) printf("%d\n", cnt); 
        else printf("-1\n"); 
    } 
    return 0; 
}