這個題目是一個好朋友給我講的方法,我按照自己的理解,敲出來代碼。 所以把算法流程和代碼貢獻出來,希望和大家共同學習。
題目大意:
給出一個柱形統計圖(histogram), 它的每個項目的寬度是1, 高度和具體問題有關。 現在編程求出在這個柱形圖中的最大面積的長方形。
例如:
7 2 1 4 5 1 3 3
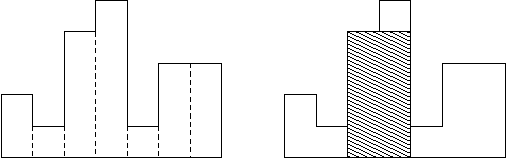
7表示柱形圖有7個數據,分別是 2 1 4 5 1 3 3, 對應的柱形圖如下,最後求出來的面積最大的圖如右圖所示。
分析:
如果采用枚舉的方式,如果當前我們枚舉項是 i = 0, 即 height = 2,
我們用另外兩個變量 j 和k 向左和向右兩個方向搜素,找到第一個 小於 height的下標,這樣我們就找到了用 i 項作為高度長方形了。
我們假設 -1位置,和最右高度都是無窮小。
例如:
i = 0, j = -1, k = 1, 最後的面積是 (k - j - 1) * height = 2
i = 1, j = -1, k = 7, 最後面積是( k - j - 1) * height = 7;
...
i = 3, j = 2, k = 5 面積是 ( k - j - 1) * height = 8
枚舉出所有的長方形的同時,然後得到最後的面積。
不過這樣的程序的時間復雜度是 O(n^2)
我們如何能僅僅做一次,就求出這個面積呢?
觀察:
當我們掃掃描到第一個高度 H1 = 2的時候,我可以標記它的起始位置1, 因為我們還不知道它將向右擴展到什麼地方,所以繼續掃面。
當遇到第二項 H2 = 1, 因為這項比之前的小,我們知道,用H1做高度的長方形結束了,算出它的面積。
同時這個時候,我們多了一個高度H2,用它做長方形高度的長方形起始位置應該是在哪裡呢? 因為H1的高度比H2要高,所以這個起始位置自然是H1所在的位置。
為了模擬上面的過程,我們引入單調棧~
我們先定義我們我們要保存的每一項數據
struct Node
{
int height;
int startPosition;
};
用來描述某一個高度,和這個高度的起始位置。
然後我們按照高度來組織成單調棧。我們來看一下它是如何工作的。
為了不用考慮堆棧為空的情況,我們用插入棧底 一個高度(0, 0)的項。
數據:
2 1 4 5 1 3 3
這樣初始化
(0 , 0)
I = 1
當掃描到(2, 1)時候,因為高度2 大於棧頂,插入
(0, 0), (2, 1)
I = 2:
當掃描到1的時候,因為1小於棧頂高度2, 我們認為棧頂的那個高度應不能再向右擴展了,所以我們將它彈出
這個時候掃描到 i = 2;
高度是 (i - 1(H1.startIndex)) * H1.height = 2;
我們得到一個面積是2的長方形。
同時我們發現高度是1的當前高度,可以擴展到 H1所在的下標,所以我們插入( 1, 1) 堆棧變成
(0, 0), (1, 1) 因為(2, 1)已經不能向右伸展了,已經被彈出了
i = 3
(0, 0), (1, 1), ( 4 3)
i = 4
(0, 0), (1, 1), (4, 3), (5, 4)
i = 5
這個時候當前高度小於棧頂高度,我們認為棧頂已經不能向右擴展,所以彈出,並且獲得面積 ( i - H5.startindex) * H5.height = (5 - 4 ) * 5 = 5
彈出這個元素後,其實(4, 3)的高度也要比 1 大,所以把這個也彈出來,同樣方式獲得面積 8.
最後我們的堆棧是
(0, 0) , (1, 1)
i = 6
(0, 0), (1, 1), ( 3, 6)
i = 7
(0, 0), (1, 1), (3, 6)
i = 8
最後一步是有點特殊的,因為我們必須要把所有的元素都彈出來,因為棧裡面的高度,都堅持到了最後,我們要把這些高度組成的長方形拿出來檢測。
我們可以假設掃面到8的時候,高度是0,(最小值)
彈出(3,6)獲得面積 (8 - 6 ) * 3 = 6
彈出(1, 1)獲得面積(8 - 1) * 1 = 7
最後的面積是8.
代碼如下:
[cpp]
Memory: 2116K Time: 454MS
Language: C++ Result: Accepted
Source Code
#include <stdio.h>
#include <stack>
using namespace std;
struct Node
{
long long height;//一個高度值
int startIdx; //這個高度值的起始位置
Node(long long _height, int _idx):height(_height), startIdx(_idx)
{
}
};
long long gHeights[100000];
long long GetMaxArea(int nItem)
{
int i;
stack<Node> s;
long long height;
s.push(Node(-1, 0));//將最小高度加入堆棧,防止堆棧彈空
int currentPosition;
long long maxArea = 0;//記錄最大面積
long long curArea;
for( i = 0; i <= nItem ; i++)
{
currentPosition = i + 1;//獲得當前 位置
if( i == nItem)//這時候,我們認為到達最後,我們要彈空棧
{
height = 0;
}
else
{
height = gHeights[currentPosition-1];
}
Node t(height, currentPosition);//當前節點
while( s.top().height > height)
{
t = s.top();
s.pop();
curArea = (currentPosition - t.startIdx) * t.height;//按照某個高度的 開始和結束的位置,獲得面積
if(curArea > maxArea)
{
maxArea = curArea;
}
}
s.push(Node(height, t.startIdx));
}
return maxArea;
}
int main()
{
int nItem;
while(scanf("%d", &nItem) != EOF && nItem)
{
int i;
for( i = 0; i < nItem; i++)
{
scanf("%lld", gHeights + i);
}
printf("%lld\n", GetMaxArea(nItem));
}
return 0;
}
作者:hopeztm