微軟等數據結構與算法面試100題第十一題

第十一題
題目：
求二叉樹中節點的最大距離...
如果我們把二叉樹看成一個圖，父子節點之間的連線看成是雙向的，
我們姑且定義"距離"為兩節點之間邊的個數。
寫一個程序，
求一棵二叉樹中相距最遠的兩個節點之間的距離。

 
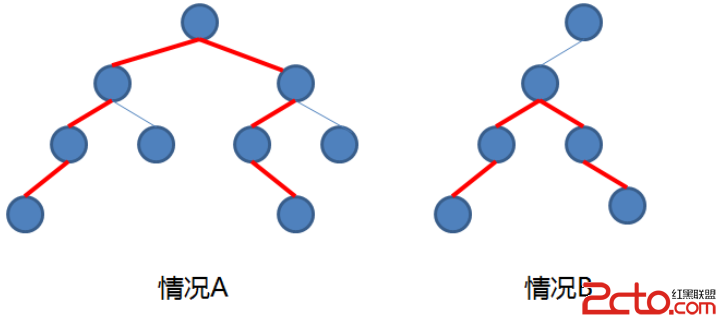
分析：
對本題而言，有上面兩種情況，一個是最大長度的節點裡面沒有根節點，一個是有根節點。
如何求解樹中節點的最大距離？-->轉換成求解每個節點的左子樹的深度和右子樹的深度問題，可以通過求解每個節點的左右子樹的深度，然後將左右深度之和作為最大長度，
然後更新最大長度。
對於圖A，根節點的左子樹的深度為3，右子樹的深度為3，因此最大長度為6，
對於圖B，不妨設根節點的左兒子節點為T，T的左子樹的深度為2，右子樹的深度為2，因此最大長度為4。
所以，我們只需要求解每個節點的左子樹深度和右子樹深度，然後不斷更新最大長度即可。

代碼：構建的二叉樹為圖A
[cpp] 
#include<iostream> 
using namespace std; 
 
struct nodeBTree 
{ 
    nodeBTree * nodeBTreeLeft; 
    nodeBTree * nodeBTreeRight; 
    int maxDepthLeft; 
    int maxDepthRight; 
    int index; 
}; 
 
int maxNum(int comp_a, int comp_b) 
{ 
    if(comp_a>comp_b)  
        return comp_a;  
    else  
        return comp_b; 
} 
void updateMaxDepthLR(nodeBTree * BTreeHead, int &MaxLength) 
{ 
    int maxDepthLC = 0; 
    int maxDepthRC = 0; 
    if(NULL==BTreeHead){return;} 
    if(NULL!=BTreeHead->nodeBTreeLeft) 
    { 
        updateMaxDepthLR(BTreeHead->nodeBTreeLeft,MaxLength); 
        maxDepthLC = max(BTreeHead->nodeBTreeLeft->maxDepthLeft,BTreeHead->nodeBTreeLeft->maxDepthRight); 
        BTreeHead->maxDepthLeft = maxDepthLC + 1; 
    } 
    else 
    { 
        BTreeHead->maxDepthLeft = 0; 
    } 
    if(NULL!=BTreeHead->nodeBTreeRight) 
    { 
        updateMaxDepthLR(BTreeHead->nodeBTreeRight,MaxLength); 
        maxDepthRC = max(BTreeHead->nodeBTreeRight->maxDepthLeft,BTreeHead->nodeBTreeRight->maxDepthRight); 
        BTreeHead->maxDepthRight = maxDepthRC + 1; 
    } 
    else 
    { 
        BTreeHead->maxDepthRight = 0; 
    } 
    if(BTreeHead->maxDepthRight + BTreeHead->maxDepthLeft >MaxLength) 
        MaxLength = BTreeHead->maxDepthRight + BTreeHead->maxDepthLeft; 
} 
int main() 
{ 
    #pragma region construct the binary tree //圖A 
    nodeBTree* a = new struct nodeBTree(); 
    a->index = 0; 
    nodeBTree* b = new struct nodeBTree(); 
    b->index = 1; 
    nodeBTree* c = new struct nodeBTree(); 
    c->index = 2; 
    nodeBTree* d = new struct nodeBTree(); 
    d->index = 3; 
    nodeBTree* e = new struct nodeBTree(); 
    e->index = 4; 
    nodeBTree* f = new struct nodeBTree(); 
    f->index = 5; 
    nodeBTree* g = new struct nodeBTree(); 
    g->index = 6; 
    nodeBTree* h = new struct nodeBTree(); 
    h->index = 7; 
    nodeBTree* i = new struct nodeBTree(); 
    i->index = 8; 
 
    a->nodeBTreeLeft = b; 
    a->nodeBTreeRight = c; 
    b->nodeBTreeLeft = d; 
    b->nodeBTreeRight = e; 
    c->nodeBTreeLeft = f; 
    c->nodeBTreeRight = g; 
    d->nodeBTreeLeft = h; 
    d->nodeBTreeRight =NULL; 
    e->nodeBTreeLeft = NULL; 
    e->nodeBTreeRight = NULL; 
    f->nodeBTreeLeft = NULL; 
    f->nodeBTreeRight = i; 
    g->nodeBTreeLeft = NULL; 
    g->nodeBTreeRight = NULL; 
    h->nodeBTreeLeft = NULL; 
    h->nodeBTreeRight = NULL; 
    i->nodeBTreeLeft = NULL; 
    i->nodeBTreeRight = NULL; 
    #pragma endregion 
 
    int MaxLength = 0; 
    updateMaxDepthLR(a,MaxLength); 
 
    //輸出update的結果 
    cout<<"a->maxDepthLeft: "<<a->maxDepthLeft<<endl; 
    cout<<"b->maxDepthLeft: "<<b->maxDepthLeft<<endl; 
    cout<<"c->maxDepthLeft: "<<c->maxDepthLeft<<endl; 
    cout<<"d->maxDepthLeft: "<<d->maxDepthLeft<<endl; 
    cout<<"e->maxDepthLeft: "<<e->maxDepthLeft<<endl; 
    cout<<"f->maxDepthLeft: "<<f->maxDepthLeft<<endl; 
    cout<<"g->maxDepthLeft: "<<g->maxDepthLeft<<endl; 
    cout<<"h->maxDepthLeft: "<<h->maxDepthLeft<<endl; 
    cout<<"i->maxDepthLeft: "<<i->maxDepthLeft<<endl; 
 
    cout<<"a->maxDepthRight: "<<a->maxDepthRight<<endl; 
    cout<<"b->maxDepthRight: "<<b->maxDepthRight<<endl; 
    cout<<"c->maxDepthRight: "<<c->maxDepthRight<<endl; 
    cout<<"d->maxDepthRight: "<<d->maxDepthRight<<endl; 
    cout<<"e->maxDepthRight: "<<e->maxDepthRight<<endl; 
    cout<<"f->maxDepthRight: "<<f->maxDepthRight<<endl; 
    cout<<"g->maxDepthRight: "<<g->maxDepthRight<<endl; 
    cout<<"h->maxDepthRight: "<<h->maxDepthRight<<endl; 
    cout<<"i->maxDepthRight: "<<i->maxDepthRight<<endl; 
 
    cout<<"MaxLength :"<<MaxLength<<endl; 
 
    return 0; 
 
}