Description
Assume the coasting is an infinite straight line. Land is in one side of coasting, sea in the other. Each small island is a point locating in the sea side. And any radar installation, locating on the coasting, can only cover d distance, so an island in the sea can be covered by a radius installation, if the distance between them is at most d.
We use Cartesian coordinate system, defining the coasting is the x-axis. The sea side is above x-axis, and the land side below. Given the position of each island in the sea, and given the distance of the coverage of the radar installation, your task is to write a program to find the minimal number of radar installations to cover all the islands. Note that the position of an island is represented by its x-y coordinates.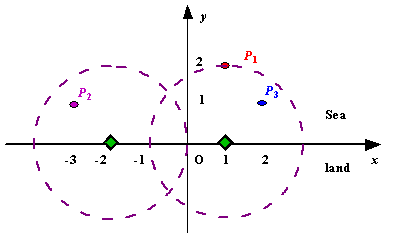
Figure A Sample Input of Radar Installations
Input
The input consists of several test cases. The first line of each case contains two integers n (1<=n<=1000) and d, where n is the number of islands in the sea and d is the distance of coverage of the radar installation. This is followed by n lines each containing two integers representing the coordinate of the position of each island. Then a blank line follows to separate the cases.
The input is terminated by a line containing pair of zeros
Output
For each test case output one line consisting of the test case number followed by the minimal number of radar installations needed. "-1" installation means no solution for that case.
Sample Input
3 2
1 2
-3 1
2 1
1 2
0 2
0 0
Sample Output
Case 1: 2
Case 2: 1
Source
Beijing 2002
求每個島對應的覆蓋它的雷達的有效區間,然後掃描區間去掉重合的。
#include <iostream>
#include <algorithm>
#include <vector>
#include <cmath>
using namespace std;
struct Island
{
int x; // 島嶼x坐標
int y; // 島嶼y坐標
double minRadarX; // 覆蓋它的雷達有效區間的左端
double maxRadarX; // 覆蓋它的雷達有效區間的右端
};
bool IslandCmp(Island & island1, Island & island2)
{
return island1.x < island2.x;
}
int main()
{
int n, d;
int caseNo = 0;
vector<Island> islandsVec;
while(cin >> n >> d)
{
islandsVec.clear();
if(n == 0 || d == 0)
break;
caseNo++;
Island island;
for(int i = 0; i < n; i++)
{
cin >> island.x >> island.y;
islandsVec.push_back(island);
}
// 按島嶼x坐標排序
sort(islandsVec.begin(), islandsVec.end(), IslandCmp);
// 求每個島嶼對應的雷達的有效區間
bool bNoAnswer = false;
vector<Island>::iterator iter;
for(iter = islandsVec.begin(); iter != islandsVec.end(); iter++)
{
if(iter->y > d)
{
bNoAnswer = true;
break;
}
double r = sqrt(d * d * 1.0 - iter->y * iter->y);
iter->minRadarX = iter->x - r;
iter->maxRadarX = iter->x + r;
}
if(bNoAnswer)
{
cout << "Case " << caseNo << ": " << -1 << endl;
}
else
{
// 統計實際需要的雷達數目
int result = 0;
double preEnd;
vector<Island>::iterator iter;
for(iter = islandsVec.begin(); iter != islandsVec.end(); iter++)
{
if(iter == islandsVec.begin())
{
result++;
preEnd = iter->maxRadarX;
}
else
{
if(iter->minRadarX > preEnd)
{
result++;
preEnd = iter->maxRadarX;
}
else
{
if(iter->maxRadarX < preEnd)
preEnd = iter->maxRadarX;
}
}
}
cout << "Case " << caseNo << ": " << result << endl;
}
}
return 0;
}