題意抽象: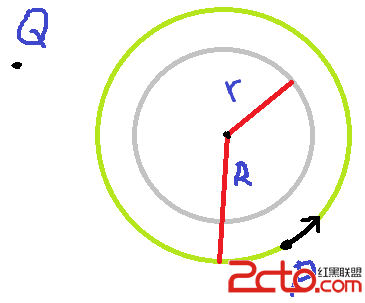
有點 p 在初始點 ( px , py ) 起逆時針等速度 p.v 沿著綠色大圓 R 轉~~點 Q 在平面上的任意位置 ( 除開灰圓 r 內 ) , 點 Q 可以沿任意方向速度最大為 Q.v 移動...灰圓 r 內部的區域是 Q 不能進入的..問 Q 和 p 最快多久能相遇....
最基本的思路是二分 , 因為若 Q 與 p 在t時間能夠相遇,那麼 >t 的時間,兩點必能一直相遇...二分時間..假設現在判斷的時間為t,那麼可以馬上得到 t 時間 p 移動到了哪個點..令這個點為 h..這時就要判斷, Q 能否在 <=t 的時間到達h點,若可以的 , 說明答案在 <=t 中 , 否則答案在 >t 中 ...
那麼關鍵之處就是判斷 Q 能否在 <=t 的時間到達h點 , 這裡分兩種情況 , 若線段 Q-h 不穿過灰圓 , 顯然 Q 最快到達 h 點就是兩點直線距離除Q.v...: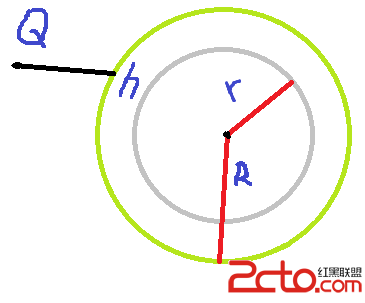
而如果線段 Q-h 穿過了灰圓 , 那麼就要繞過灰圓 , 而此時的最佳方案 :
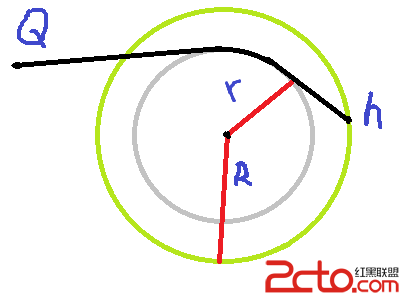
從 Q 作對於灰圓的切線 , 從 h 作對於灰圓的切線 , 兩切點之間 貼著灰圓的邊 ( 較短的弧長 ) 過去..易證此時路徑是最短的...
當然這題有很多細節要注意...比如如何求出 t 時間的 h 點..如何判斷線段 Q-h 是否過灰圓...如何得到兩切點間弧長的大小....
Program:
[cpp]
#include<iostream>
#include<stdio.h>
#include<algorithm>
#include<string.h>
#include<math.h>
#include<queue>
#include<stack>
#define ll long long
#define pi acos(-1)
using namespace std;
struct node
{
double x,y,v,r;
}p,Q,h,D;
double mid,l,r,alp,thelen;
double l1,l2,l3,a1;
double dis(node a,node b)
{
return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));
}
bool CorssTheCircle(node a,node b)
{
double d1=fabs(a.x*b.y-b.x*a.y)/dis(a,b),d2,d3,d4;
if (a1<1e-10 || d1-Q.r>-1e-10) return true;
return false;
}
double judge(double t)
{
double a=p.v*t+alp,t1;
h.x=p.r*cos(a);
h.y=p.r*sin(a);
l1=(Q.x*Q.x)+(Q.y*Q.y);
l2=(h.x*h.x)+(h.y*h.y);
l3=(Q.x-h.x)*(Q.x-h.x)+(Q.y-h.y)*(Q.y-h.y);
a1=acos((l1+l2-l3)/(2*sqrt(l1)*sqrt(l2)))-acos(Q.r/sqrt(l1))-acos(Q.r/sqrt(l2));
if (CorssTheCircle(Q,h)) t1=dis(h,Q);
else t1=sqrt(l1-Q.r*Q.r)+sqrt(l2-Q.r*Q.r)+thelen*a1/(2*pi);
t1/=Q.v;
if (t1<t) return false;
return true;
}
int main()
{
while (~scanf("%lf%lf%lf",&p.x,&p.y,&p.v))
{
scanf("%lf%lf%lf%lf",&Q.x,&Q.y,&Q.v,&Q.r);
thelen=2*pi*Q.r;
p.r=sqrt(p.x*p.x+p.y*p.y);
D.x=D.y=0;
alp=acos(p.x/p.r);
if (p.y<0) alp=-alp;
p.v/=p.r;
l=0; r=1e+10;
while (r-l>1e-12)
{
mid=(l+r)*0.5;
if (judge(mid)) l=mid;
else r=mid;
}
printf("%.9lf\n",l);
}
return 0;
}