Square Destroyer
Time Limit: 1000MS Memory Limit: 10000K
Total Submissions: 2695 Accepted: 1101
Description
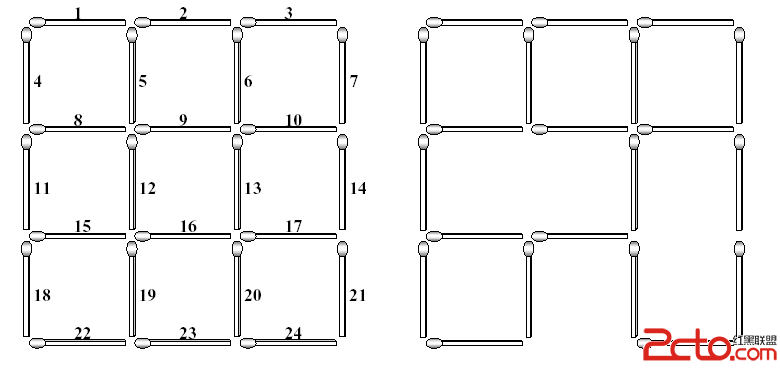
The left figure below shows a complete 3*3 grid made with 2*(3*4) (=24) matchsticks. The lengths of all matchsticks are one. You can find many squares of different sizes in the grid. The size of a square is the length of its side. In the grid shown in the left figure, there are 9 squares of size one, 4 squares of size two, and 1 square of size three.
Each matchstick of the complete grid is identified with a unique number which is assigned from left to right and from top to bottom as shown in the left figure. If you take some matchsticks out from the complete grid, then some squares in the grid will be destroyed, which results in an incomplete 3*3 grid. The right figure illustrates an incomplete 3*3 grid after removing three matchsticks numbered with 12, 17 and 23. This removal destroys 5 squares of size one, 3 squares of size two, and 1 square of size three. Consequently, the incomplete grid does not have squares of size three, but still has 4 squares of size one and 1 square of size two.
As input, you are given a (complete or incomplete) n*n grid made with no more than 2n(n+1) matchsticks for a natural number 5 <= n . Your task is to compute the minimum number of matchsticks taken
out to destroy all the squares existing in the input n*n grid.
Input
The input consists of T test cases. The number of test cases (T ) is given in the first line of the input file.
Each test case consists of two lines: The first line contains a natural number n , not greater than 5, which implies you are given a (complete or incomplete) n*n grid as input, and the second line begins with a nonnegative integer k , the number of matchsticks that are missing from the complete n*n grid, followed by
k numbers specifying the matchsticks. Note that if k is equal to zero, then the input grid is a complete n*n grid; otherwise, the input grid is an incomplete n*n grid such that the specified k matchsticks are missing from the complete n*n grid.
Output
Print exactly one line for each test case. The line should contain the minimum number of matchsticks that have to be taken out to destroy all the squares in the input grid.
Sample Input
2
2
0
3
3 12 17 23
Sample Output
3
3
Source
Taejon 2001
Dancing Links重復覆蓋,難在如何構建0/1矩陣。把火柴桿作為行,圖中存在的正方形作為列,如果第i根火柴是第j個正方形的邊的一部分,那麼mtx[i][j] = 1;否則,mtx[i][j] = 0。
[cpp]
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
using namespace std;
const int maxn = 65*6*6*6;
const int oo = 1 << 30;
const int maxrow = 65;
const int maxcol = 6*6*6;
bool mtx[maxrow][maxcol];
int t, n, k, ans;
int has[65];
int totRow, totCol, head, idx;
int L[maxn], R[maxn], U[maxn], D[maxn];
int RH[maxn], CH[maxn], S[maxn];
bool ok(int x1, int y1, int x2, int y2)
{
bool flag = true;
int id;
for (int i = y1; i <= y2; ++i) {
id = (x1 - 1) * (2 * n + 1) + i;
if (!has[id]) {
flag = false;
break;
}
id = (x2) * (2 * n + 1) + i;
if (!has[id]) {
flag = false;
break;
}
}
if (!flag) return false;
for (int i = x1; i <= x2; ++i) {
id = (i - 1)*(2*n+1) + n + y1;
if (!has[id]) {
flag = false;
break;
}
id = (i - 1)*(2*n+1) + n + y2 + 1;
if (!has[id]) {
flag = false;
break;
}
}
if (!flag) return false;
return true;
}
void add(int x1, int y1, int x2, int y2, int c)
{
int id;
for (int i = y1; i <= y2; ++i) {
id = (x1 - 1) * (2 * n + 1) + i;
mtx[id-1][c] = 1;
id = (x2) * (2 * n + 1) + i;
mtx[id-1][c] = 1;
}
for (int i = x1; i <= x2; ++i) {
id = (i - 1)*(2*n+1) + n + y1;
mtx[id-1][c] = 1;
id = (i - 1)*(2*n+1) + n + y2 + 1;
mtx[id-1][c] = 1;
}
}
void initMtx()
{
int cnt = 0;
memset(mtx, 0, sizeof(mtx));
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= n; ++j) {
for (int k = 0; i + k <= n && j + k <= n; ++k) {
if (ok(i, j, i + k, j + k)) {
add(i, j, i + k, j + k, cnt);
cnt++;
}
}
}
}
totRow = 2 * n * (n + 1);
totCol = cnt;
}
int newNode(int up, int down, int left, int right)
{
U[idx] = up; D[idx] = down;
L[idx] = left; R[idx] = right;
U[down] = D[up] = L[right] = R[left] = idx;
return idx++;
}
void build()
{
idx = maxn - 1;
head = newNode(idx, idx, idx, idx);
idx = 0;
for (int j = 0; j < totCol; ++j) {
newNode(idx, idx, L[head], head);
CH[j] = j; S[j] = 0;
}
for (int i = 0; i < totRow; ++i) {
int k = -1;
for (int j = 0; j < totCol; ++j) {
if (!mtx[i][j]) continue;
if (-1 == k) {
k = newNode(U[CH[j]], CH[j], idx, idx);
RH[k] = i; CH[k] = j; S[j]++;
} else {
k = newNode(U[CH[j]], CH[j], k, R[k]);
RH[k] = i; CH[k] = j; S[j]++;
}
}
}
}
void remove(int c)
{
for (int i = D[c]; i != c; i = D[i]) {
L[R[i]] = L[i]; R[L[i]] = R[i]; /*S[CH[i]]--;*/
}
}
void resume(int c)
{
for (int i = U[c]; i != c; i = U[i]) {
L[R[i]] = R[L[i]] = i; /*S[CH[i]]++;*/
}
}
/*估價函數*/
int h()
{
bool vis[maxcol];
memset(vis, false, sizeof(vis));
int ret = 0;
for (int i = R[head]; i != head; i = R[i]) {
if (!vis[i]) {
ret++;
vis[i] = true;
for (int j = D[i]; j != i; j = D[j]) {
for (int k = R[j]; k != j; k = R[k]) {
vis[CH[k]] = true;
}
}
}
}
return ret;
}
void dance(int cnt)
{
if (cnt + h() >= ans) {
return ;
}
if (R[head] == head) {
ans = cnt;
return ;
}
int c, Min = oo;
for (int i = R[head]; i != head; i = R[i]) {
if (S[i] < Min) {
Min = S[i]; c = i;
}
}
for (int i = D[c]; i != c; i = D[i]) {
remove(i);
for (int j = R[i]; j != i; j = R[j]) {
remove(j);
}
dance(cnt + 1);
for (int j = L[i]; j != i; j = L[j]) {
resume(j);
}
resume(i);
}
return ;
}
int main()
{
scanf("%d", &t);
while (t--) {
scanf("%d", &n);
scanf("%d", &k);
memset(has, true, sizeof(has));
int num;
for (int i = 0; i < k; ++i) {
scanf("%d", &num);
has[num] = false;
}
initMtx();
build();
ans = oo;
dance(0);
printf("%d\n", ans);
}
return 0;
}