求最大獨立集 = n (頂點數)- 最大匹配/2(這裡的最大匹配因為是無向圖,所以除2)
(轉)本題中的A集合為頂點集,B集合也為頂點集並且例如(1--2)和(2--1)並存,那麼接下來我們有兩種選擇,去掉其中一個,向公式靠攏;
或者二者並存,變換一下公式。為了處理的方便,我們選擇二者並存,那麼我們求出的最大匹配數其實是真實的平匹配數的二倍對於此種情況下有:最大獨立集=頂點數-最大匹配數/2
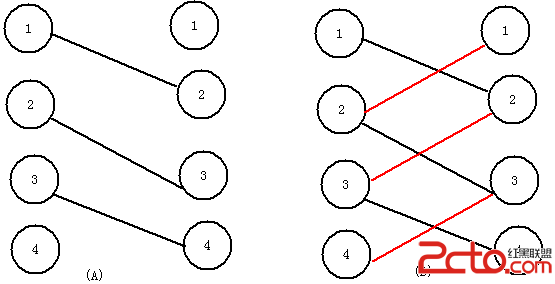
A圖(屬於上面提到的前者) B圖(屬於上面提到的後者 紅線代表多余的邊) 顯然圖B的最大匹配數是圖A的二倍
下面是AC代碼:
[cpp]
#include<cstdio>
#include<cstring>
using namespace std;
const int maxn = 1100;
int n,m;
int g[maxn][maxn];
int match[maxn];
bool vis[maxn];
bool dfs(int cur){
for(int i=1;i<=n;i++){
if(g[cur][i]&&!vis[i]){
vis[i]=true;
int t=match[i];
if(t==-1||dfs(t)){
match[i]=cur;
return true;
}
}
}
return false;
}
int hungary(){
for(int i=1;i<=n;i++) match[i]=-1;
int res=0;
for(int i=1;i<=n;i++){
memset(vis,false,sizeof(vis));
if(dfs(i))
res++;
}
return res;
}
int main(){
int t,x,y,id,num;
while(scanf("%d",&n)!=EOF){
memset(g,0,sizeof(g));
for(int i=0;i<n;i++){
scanf("%d: (%d)",&id,&num);
id++;
for(int j=1;j<=num;j++){
scanf("%d",&x);
x++;
g[x][id]=g[id][x]=1;
}
}
printf("%d\n",n-hungary()/2);
}
return 0;
}