給定有n個要相乘的矩陣構成的序列(鏈)<A1,A2,A3,.......,An>,要計算乘積A1A2.....An。一組矩陣是加全部括號的。矩陣鏈加括號對運算的性能有很大影響。
僅當兩個矩陣A和B相容(即A的列數等於B的行數),才可以進行相乘運算。如果A是一個p×q矩陣,B是q×r矩陣,結果C是p×r的矩陣。計算C的時間由乘法運算次數決定的,次數為p×q×r。
矩陣鏈乘法問題可表述為:給定n個矩陣構成的一個鏈<A1,A2,A3.......,An>,其中i=1,2,3,4.....,n,矩陣Ai的維數為Pi-1 ×Pi,對乘積A1A2A3.....An,以一種最小標量乘法次數的方式進行加全部括號。
對AiAi+1.......Aj的任何家全部括號形式都將乘積在Ak和Ak+1之間分開,即計算矩陣Ai...k和Ak+1.....Aj,然後將他們相乘得到最終的乘積Ai.......j.加全括號的代價是Ai...k和Ak+1...j的代價之和,再加上兩者相乘的代價。
加全部括號最小代價的遞歸定義:
m[i,j]=min{m[i,k] + m[k+1,j] + Pi-1 * Pk *Pj} ;i<j; m[i,j]=0; i==j;
計算最優代價時,使用輔助表m[n][n]來保存m[i][j],使用s[n][n]來記錄計算m[i][j]時取得的最優代價處的k值,即每一個表項s[i][j]都記錄了對乘積AiAi+1......Aj在Ak和Ak+1之間進行分裂取得的最優加全部括號時的k值。
全部代碼如下:
[cpp]
//計算矩陣鏈乘積所需的最有標量乘法次數
void MATRIX_CHAIN_ORDER(int PArray[], int m[][PArrayLength], int s[][PArrayLength], int Length)
{
int n=Length-1;//表示有n個矩陣相乘
int temp=0;//臨時變量
for (int i=1; i<Length; i++)
{
m[i][i]=0;//先將代價初始化為0;長度為1的鏈最小代價為0
}
for (int l=2; l<=n; l++)//從第二個鏈開始分別計算長度為2、3、。。n的鏈的最小代價
{
for (int i=1; i<=n-l+1; i++)
{
int j=i+l-1;
m[i][j]=0x7fffffff;
for(int k=i; k<j; k++)//逐個檢驗K值,找到最小代價的k值
{
temp=m[i][k]+m[k+1][j]+PArray[i-1]*PArray[k]*PArray[j];
if (temp<m[i][j])
{
m[i][j]=temp;
s[i][j]=k;
}
}
}
}
}
//構造一個最優解
void PRINT_OPTIMAL_PARENS(int s[][PArrayLength], int i, int j)
{
if (i==j)
{
cout<<"A"<<i;
}
else
{
cout<<"(";
PRINT_OPTIMAL_PARENS(s, i, s[i][j]);
PRINT_OPTIMAL_PARENS(s, s[i][j]+1, j);
cout<<")";
}
}
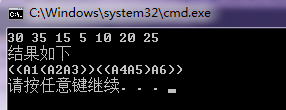
結果: