堆常用來實現優先隊列,在這種隊列中,待刪除的元素為優先級最高(最低)的那個。在任何時候,任意優先元素都是可以插入到隊列中去的,是計算機科學中一類特殊的數據結構的統稱
一、堆的定義
最大(最小)堆是一棵每一個節點的鍵值都不小於(大於)其孩子(如果存在)的鍵值的樹。大頂堆是一棵完全二叉樹,同時也是一棵最大樹。小頂堆是一棵完全完全二叉樹,同時也是一棵最小樹。
注意:
堆中任一子樹亦是堆。
以上討論的堆實際上是二叉堆(Binary Heap),類似地可定義k叉堆。
下圖分別給出幾個最大堆和最小堆的例子:
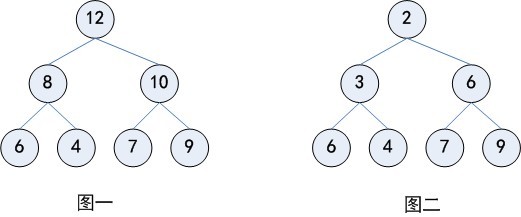
二、支持的基本操作
堆支持以下的基本操作:
build: 建立一個空堆;
insert: 向堆中插入一個新元素;
update:將新元素提升使其符合堆的性質;
get:獲取當前堆頂元素的值;
delete:刪除堆頂元素;
heapify:使刪除堆頂元素的堆再次成為堆。
某些堆實現還支持其他的一些操作,如斐波那契堆支持檢查一個堆中是否存在某個元素。
三、堆的應用
1.堆排序
堆排序(HeapSort)是一樹形選擇排序。 www.2cto.com
堆排序的特點是:在排序過程中,將R[l..n]看成是一棵完全二叉樹的順序存儲結構,利用完全二叉樹中雙親結點和孩子結點之間的內在關系【參見二叉樹的順序存儲結構】,在當前無序區中選擇關鍵字最大(或最小)的記錄。
優點直接選擇排序中,為了從R[1..n]中選出關鍵字最小的記錄,必須進行n-1次比較,然後在R[2..n]中選出關鍵字最小的記錄,又需要做n-2次比較。事實上,後面的n-2次比較中,有許多比較可能在前面的n-1次比較中已經做過,但由於前一趟排序時未保留這些比較結果,所以後一趟排序時又重復執行了這些比較操作。
堆排序可通過樹形結構保存部分比較結果,可減少比較次數。
堆排序利用了大根堆(或小根堆)堆頂記錄的關鍵字最大(或最小)這一特征,使得在當前無序區中選取最大(或最小)關鍵字的記錄變得簡單。
(1)、用大根堆排序的基本思想
先將初始文件R[1..n]建成一個大根堆,此堆為初始的無序區
再將關鍵字最大的記錄R[1](即堆頂)和無序區的最後一個記錄R[n]交換,由此得到新的無序區R[1..n-1]和有序區R[n],且滿足R[1..n-1].keys≤R[n].key
由於交換後新的根R[1]可能違反堆性質,故應將當前無序區R[1..n-1]調整為堆。然後再次將R[1..n-1]中關鍵字最大的記錄R[1]和該區間的最後一個記錄R[n-1]交換,由此得到新的無序區R[1..n-2]和有序區R[n-1..n],且仍滿足關系R[1..n-2].keys≤R[n-1..n].keys,同樣要將R[1..n-2]調整為堆。直到無序區只有一個元素為止。
(2)、大根堆排序算法的基本操作:
初始化操作:將R[1..n]構造為初始堆;
每一趟排序的基本操作:將當前無序區的堆頂記錄R[1]和該區間的最後一個記錄交換,然後將新的無序區調整為堆(亦稱重建堆)。
注意:
只需做n-1趟排序,選出較大的n-1個關鍵字即可以使得文件遞增有序。
用小根堆排序與利用大根堆類似,只不過其排序結果是遞減有序的。堆排序和直接選擇排序相反:在任何時刻,堆排序中無序區總是在有序區之前,且有序區是在原向量的尾部由後往前逐步擴大至整個向量為止。
(3)、算法實現
[cpp]
////////////////////////////////////////////////////////////////////
//堆排序
template <class T>
void Sort::HeapSort(T arr[], int len){
int i;
//建立子堆
for(i = len / 2; i >= 1; i--){
CreateHeap(arr, i, len);
}
for(i = len - 1; i >= 1; i--){
buff = arr[1];
arr[1] = arr[i + 1];
arr[i + 1] = buff;
CreateHeap(arr, 1, i);
}
}
//建立堆
template <class T>
void Sort::CreateHeap(T arr[], int root, int len){
int j = 2 * root; //root's left child, right (2 * root + 1)
T temp = arr[root];
bool flags = false;
while(j <= len && !flags){
if(j < len){
if(arr[j] < arr[j + 1]){ // Left child is less then right child
++j; // Move the index to the right child
}
}
if(temp < arr[j]){
arr[j / 2] = arr[j];
j *= 2;
}else{
flags = true;
}
}
arr[j / 2] = temp;
}
////////////////////////////////////////////////////////////////////
//堆排序
template <class T>
void Sort::HeapSort(T arr[], int len){
int i;
//建立子堆
for(i = len / 2; i >= 1; i--){
CreateHeap(arr, i, len);
}
for(i = len - 1; i >= 1; i--){
buff = arr[1];
arr[1] = arr[i + 1];
arr[i + 1] = buff;
CreateHeap(arr, 1, i);
}
}
//建立堆
template <class T>
void Sort::CreateHeap(T arr[], int root, int len){
int j = 2 * root; //root's left child, right (2 * root + 1)
T temp = arr[root];
bool flags = false;
while(j <= len && !flags){
if(j < len){
if(arr[j] < arr[j + 1]){ // Left child is less then right child
++j; // Move the index to the right child
}
}
if(temp < arr[j]){
arr[j / 2] = arr[j];
j *= 2;
}else{
flags = true;
}
}
arr[j / 2] = temp;
} 2.選擇前k個最大(最小)的數
思想:在一個很大的無序數組裡面選擇前k個最大(最小)的數據,最直觀的做法是把數組裡面的數據全部排好序,然後輸出前面最大(最小)的k個數據。但是,排序最好需要O(nlogn)的時間,而且我們不需要前k個最大(最小)的元素是有序的。這個時候我們可以建立k個元素的最小堆(得出前k個最大值)或者最大堆(得到前k個最小值),我們只需要遍歷一遍數組,在把元素插入到堆中去只需要logk的時間,這個速度是很樂觀的。利用堆得出前k個最大(最小)元素特別適合海量數據的處理。
代碼:
[cpp]
typedef multiset<int, greater<int> > intSet;
typedef multiset<int, greater<int> >::iterator setIterator;
void GetLeastNumbers(const vector<int>& data, intSet& leastNumbers, int k)
{
leastNumbers.clear();
if(k < 1 || data.size() < k)
return;
vector<int>::const_iterator iter = data.begin();
for(; iter != data.end(); ++ iter)
{
if((leastNumbers.size()) < k)
leastNumbers.insert(*iter);
else
{
setIterator iterGreatest = leastNumbers.begin();
if(*iter < *(leastNumbers.begin()))
{
leastNumbers.erase(iterGreatest);
leastNumbers.insert(*iter);
}
}
}