題目:
Here We Go(relians) Again
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 360 Accepted Submission(s): 204
Problem Description
The Gorelians are a warlike race that travel the universe conquering new worlds as a form of recreation. Given their violent, fun-loving nature, keeping their leaders alive is of serious concern. Part of the Gorelian security plan involves changing the traffic patterns of their cities on a daily basis, and routing all Gorelian Government Officials to the Government Building by the fastest possible route.
Fortunately for the Gorelian Minister of Traffic (that would be you), all Gorelian cities are laid out as a rectangular grid of blocks, where each block is a square measuring 2520 rels per side (a rel is the Gorelian Official Unit of Distance). The speed limit between two adjacent intersections is always constant, and may range from 1 to 9 rels per blip (a blip, of course, being the Gorelian Official Unit of Time). Since Gorelians have outlawed decimal numbers as unholy (hey, if you're the dominant force in the known universe, you can outlaw whatever you want), speed limits are always integer values. This explains why Gorelian blocks are precisely 2520 rels in length: 2520 is the least common multiple of the integers 1 through 9. Thus, the time required to travel between two adjacent intersections is always an integer number of blips.
In all Gorelian cities, Government Housing is always at the northwest corner of the city, while the Government Building is always at the southeast corner. Streets between intersections might be one-way or two-way, or possibly even closed for repair (all this tinkering with traffic patterns causes a lot of accidents). Your job, given the details of speed limits, street directions, and street closures for a Gorelian city, is to determine the fastest route from Government Housing to the Government Building. (It is possible, due to street directions and closures, that no route exists, in which case a Gorelian Official Temporary Holiday is declared, and the Gorelian Officials take the day off.)
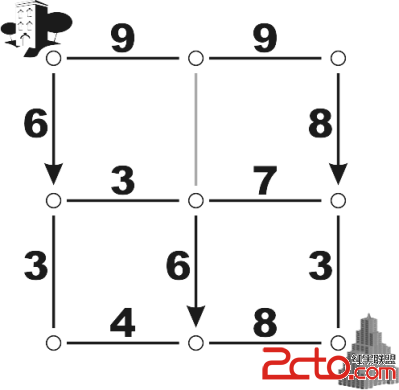
The picture above shows a Gorelian City marked with speed limits, one way streets, and one closed street. It is assumed that streets are always traveled at the exact posted speed limit, and that turning a corner takes zero time. Under these conditions, you should be able to determine that the fastest route from Government Housing to the Government Building in this city is 1715 blips. And if the next day, the only change is that the closed road is opened to two way traffic at 9 rels per blip, the fastest route becomes 1295 blips. On the other hand, suppose the three one-way streets are switched from southbound to northbound (with the closed road remaining closed). In that case, no route would be possible and the day would be declared a holiday.
Input
The input consists of a set of cities for which you must find a fastest route if one exists. The first line of an input case contains two integers, which are the vertical and horizontal number of city blocks, respectively. The smallest city is a single block, or 1 by 1, and the largest city is 20 by 20 blocks. The remainder of the input specifies speed limits and traffic directions for streets between intersections, one row of street segments at a time. The first line of the input (after the dimensions line) contains the data for the northernmost east-west street segments. The next line contains the data for the northernmost row of north-south street segments. Then the next row of east-west streets, then north-south streets, and so on, until the southernmost row of east-west streets. Speed limits and directions of travel are specified in order from west to east, and each consists of an integer from 0 to 9 indicating speed limit, and a symbol indicating which direction traffic may flow. A zero speed limit means the road is closed. All digits and symbols are delimited by a single space. For east-west streets, the symbol will be an asterisk '*' which indicates travel is allowed in both directions, a less-than symbol '<' which indicates travel is allowed only in an east-to-west direction, or a greater-than symbol '>' which indicates travel is allowed only in a west-to-east direction. For north-south streets, an asterisk again indicates travel is allowed in either direction, a lowercase "vee" character 'v' indicates travel is allowed only in a north-to-south directions, and a caret symbol '^' indicates travel is allowed only in a south-to-north direction. A zero speed, indicating a closed road, is always followed by an asterisk. Input cities continue in this manner until a value of zero is specified for both the vertical and horizontal dimensions.
Output
For each input scenario, output a line specifying the integer number of blips of the shortest route, a space, and then the word "blips". For scenarios which have no route, output a line with the word "Holiday".
Sample Input
2 2
9 * 9 *
6 v 0 * 8 v
3 * 7 *
3 * 6 v 3 *
4 * 8 *
2 2
9 * 9 *
6 v 9 * 8 v
3 * 7 *
3 * 6 v 3 *
4 * 8 *
2 2
9 * 9 *
6 ^ 0 * 8 ^
3 * 7 *
3 * 6 ^ 3 *
4 * 8 *
0 0
Sample Output
1715 blips
1295 blips
Holiday
題目大意:
題目讀得有點惡心。n*m大小的矩形,起點在矩形的左上角, 終點在右下角,裡面一個小矩形代表一個街區(block)。每個小矩形的邊長都是2520, 小矩形的邊有一個速度限制,范圍是0~9, 如果是0表示這條邊不能行駛。
關於輸入部分,也確實夠惡心的,由上到下,從左到右,按照上圖的對應的位置方式給出數據, 每一條邊是 "數字"+“空格”+“符號”的形式, 數字表示這條邊的限速, 符號表示這條路是單向(還分東西, 南北)的還是雙向的。
分析與總結:
這題的關鍵在於讀題以及處理輸入, 建完圖之後隨便用哪個最短路算法都行,愛啥啥。
代碼:
[cpp]
#include<iostream>
#include<cstdio>
#include<cstring>
#include<queue>
#include<utility>
using namespace std;
typedef pair<int,int>pii;
const int INF = 0x7fffffff;
const int VN = 445;
const int EN = VN*VN/2;
struct Edge{
int v, next, w;
}E[EN];
int n;
int m;
int vn;
int size;
int head[VN];
int d[VN];
void addEdge(int u,int v,int w){
E[size].v=v;
E[size].w=w;
E[size].next=head[u];
head[u]=size++;
}
void init(){
vn=(m+1)*(n+1);
size=0;
memset(head, -1, sizeof(head));
}
void Dijkstra(int src){
for(int i=1; i<=vn; ++i)d[i]=INF;
d[src]=0;
priority_queue<pii,vector<pii>,greater<pii> >q;
q.push(make_pair(d[src],src));
while(!q.empty()){
pii x = q.top(); q.pop();
int u=x.second;
if(d[u]!=x.first)continue;
for(int e=head[u]; e!=-1; e=E[e].next){
int tmp=d[u]+E[e].w;
if(d[E[e].v] > tmp){
d[E[e].v] = tmp;
q.push(make_pair(tmp,E[e].v));
}
}
}
}
int main(){
char str[100];
int u,v,w;
while(~scanf("%d%d%*c",&n,&m)&&n+m){
// input
init();
for(int i=1; i<=n*2+1; ++i){
gets(str);
int len=strlen(str);
if(i&1){
for(int j=0,k=1; j<len; j+=4,++k){
u=(m+1)*(i/2)+k;
w = str[j]-'0';
if(w==0)continue;
if(str[j+2]=='*'){
addEdge(u,u+1,2520/w);
addEdge(u+1,u,2520/w);
}
else if(str[j+2]=='<'){
addEdge(u+1,u,2520/w);
}
else{
addEdge(u,u+1,2520/w);
}
}
}
else{
for(int j=0,k=1; j<len; j+=4,++k){
u = (m+1)*(i/2-1)+k;
w = str[j]-'0';
if(w==0) continue;
if(str[j+2]=='*'){
addEdge(u, u+m+1, 2520/w);
addEdge(u+m+1, u, 2520/w);
}
else if(str[j+2]=='v'){
addEdge(u, u+m+1, 2520/w);
}
else if(str[j+2]=='^'){
addEdge(u+m+1, u, 2520/w);
}
}
}
}
Dijkstra(1);
if(d[vn]!=INF) printf("%d blips\n", d[vn]);
else puts("Holiday");
}
return 0;
}